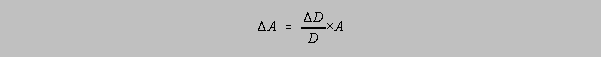
SIGNIFICANT FIGURES OR DIGITS
Any quantitative measurement of a property requires the placing of a numerical value on that
property and also a statement of the units in which the measurement is made (cm, g, mL etc.) The
number of digits used to designate the numerical value is referred to as the number of significant
figures or digits, and these depend upon the precision of the measuring device. Valuable
information may be lost if digits that are significant are omitted. It is equally wrong to record
too
many digits, since this implies greater precision than really exists.
Thus, significant figures are those digits that give meaningful but not misleading
information.
Only the last digit contains an uncertainty, which is due to the precision of the measurement.
Therefore, when a measurement is made and the precision of the measurement is considered, all
digits thought to be reasonably reliable are significant. For example:
2.05 has three significant figures
64.472 has five significant figure
0.74 has two significant figures
Zeroes may or may not be significant. The following rules should be helpful:
1. A zero between two digits is significant. 107.8 has four significant figures
2. Final zeroes after a decimal point are always significant. 1.5000 has five significant figures
3. Zeroes are not significant when they are used to fix the position of the decimal point. 0.0031 has two significant figures
4. Some notations are ambiguous and should be avoided, for instance for a number such as 700 it is not clear how many digits are significant. This ambiguity can be avoided by the use of scientific notation.
It is important to realize that significant digits are taken to be all digits that are certain plus
one
digit, namely the last one, which has an uncertainty of plus or minus one in that place. The
left-most digit in a number is said to be the most-significantdigit (msd) and the right-most digit is
the least-significant-digit (lsd). For another discussion of this topic see pages 39-40 in SHW.
SIGNIFICANT FIGURES FOR A SUM OR DIFFERENCE
When adding or subtracting significant figures, the answer is expressed only as far as the last
complete column of digits. Here are some examples:
15.42+0.307=15.73
3.43+8.6=12.0
27.0-0.364=26.6
SIGNIFICANT FIGURES FOR A PRODUCT OR QUOTIENT
It is often stated that the number of significant digits in the answer should be the same as the
number of significant digits in the datum which has the smallest number of significant digits.
For
example for the result of the following division 9.8/9.41 = 1.0414 the result, according to the
above rule should be rounded to two significant digits since the datum with the fewest significant
digits, namely 9.8 has only two digits. This rule which is often quoted and one that many
students
find familiar and simple suffers from a serious defect. The relative uncertainty of the two pieces
of data is quite different. For 9.8 it is 1/98 0.01, while for 9.41 it is 1/941 0.001. Clearly, the
answer should not show a relative uncertainty smaller than the largest relative uncertainty in the
data. Conversely, the answer should not be given in such a manner that its relative uncertainty is
larger that warranted by the data. In the example given the application of the common rule
would
indicate that the answer should have two significant digits, i.e. it should be 1.0. The relative
uncertainty then would be 1/10 = 0.1, which is far larger than 0.01. For this reason it appears that
a more sophisticated rule, which considers the relative uncertainties of both data and answer, is
needed. A relatively simple rule which does this can be derived from the following
considerations.
For single and chained multiplications, and to a good approximation for divisions, the
uncertainty
in A is related to the uncertainty in D by:
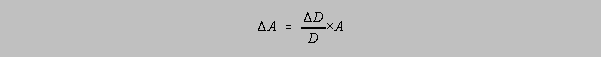
The relative uncertainty in D is equal to the relative uncertainty in A.
The improved product-quotient rule, based on the preceding analysis, is given below.
1. Identify the datum with the fewest number of digits, or, if two or more data are given to
the same number of digits, the one that is the smallest number when the decimal point is ignored.
Write out the digits, of the datum so determined, as an integer number, ignoring the decimal
point.
2. Divide this integer into the answer and note the most significant digit in the result. The
position of this digit is the position of the last digit that should be preserved in the answer.
In the above example 9.8 is clearly the datum with the fewest number of digits. One
therefore
divides 1.0414 by 98 obtaining 0.01063. The most significant digit in this answer is in the
hundredth's place. The result of dividing 9.8 by 9.41 should be expressed with the least
significant
digit in the hundredth's place, i.e. 1.04. Note that the relative uncertainty of this result is 1/104
0.01, which is precisely the relative uncertainty in 9.8.
SIGNIFICANT FIGURES FOR POWERS AND ROOTS
Let A = KDa, where K is a constant and "a" is a constant exponent, either
integral or fractional. It
can be shown that the relative uncertainty in A is equal to the relative uncertainty in D multiplied
by "a", i.e.
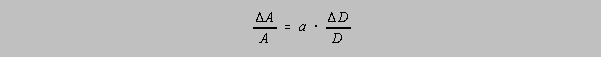
For example, let A = (0. 0768)1/4 = 0.52643.... Then
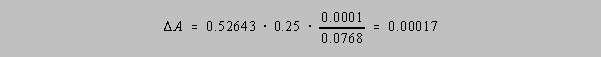
Since the most significant digit in the latter answer appears in the fourth decimal place, the
correct
number of significant figures in A is four, i.e. A = 0.5264.
SIGNIFICANT FIGURES FOR LOGARITHMS AND ANTI-LOGARITHMS
Given a [H+] = 1. 8 x 10-4 we can calculate the pH from the definition of quantity, i.e.
pH = -log[H+]. How many significant should the pH show?
A logarithm consists of two parts. Digits to the left of the decimal point, these digits are
known
as the characteristic. The characteristic is not a significant digit since it only indicates the
magnitude of the number. The digits to the right of the decimal point are the mantissa and they
represent the accuracy to which a result is known. This then suggests the following rules:
1. When calculating a logarithm, retain in the mantissa the same number of significant
digits
as were present in the original datum.
2. When calculating an anti-logarithm retain the same number of significant figures as
were
present in the mantissa of the logarithm.
3. Note that all zeros in a mantissa are significant regardless of position.
ROUNDING OF NUMBERS
When we use significant figures in numerical operations, we often obtain answers with more digits than are justified. We must then round the answers to the correct number of significant digits by dropping extraneous digits. Use the following rules for rounding purposes:
1. If the digit to be dropped is 0, 1, 2, 3 or 4 drop it and leave the last remaining digit as it
is.
2. If the digit to be dropped is 5, 6, 7, 8 or 9 increase the last remaining digit by 1.
The above rules can be summarized as follows: "If the first (leftmost) digit to be dropped is
significant and is 5-9 round up, otherwise truncate. It is important to realize that rounding must
be postponed until the calculation is complete, i.e. do not round intermediate results.
ACCURACY VS. PRECISION
Experimental determination of any quantity is subject to error because it is impossible to carry out any measurement with absolute certainty. The extent of error in any determination is a function of the quality of the instrument or the measuring device, the skill and experience of the experimenter. Thus, discussion of errors is an essential part of experimental work in any quantitative science.
The types of errors encountered in making measurements are classified into three groups:
1. Gross, careless errors are those due to mistakes that are not likely to be
repeated
in similar
determinations. These include the spilling of a sample, reading the weight incorrectly, reading a
buret volume incorrectly, etc..
2. Random errors. also called indeterminate errors. are due to the
inherent
limitations of the
equipment or types of observations being made. These types of errors may also be due to lack of
care by the experimenter. Generally these can be minimized by using high-grade equipment and
by careful work with this equipment but can never be completely eliminated. It is customary to
perform measurements in replicate in order to reduce the effect of random errors on the
determination.
3. Systematic errors, also called determinate errors, are those that affect
each individual
result of replicate determinations in exactly the same way. They may be errors of the measuring
instrument, of the observer or of the method itself. Examples of errors in chemical analyses
include such things as the use of impure materials for standardization of solutions, improperly
calibrated volumetric glassware such as pipets, burets and volumetric flasks.
Students can recognize the occurrence of careless or random errors by deviations of the
separate
determinations from each other. This is called the precision of the measurement. The
existence
of systematic errors is realized when the experimental results are compared with the true value.
This is the accuracy of the result. A further discussion of these terms is given below:
Accuracy of a measurement refers to the nearness of a numerical value to the correct
or accepted
value. It is often expressed in terms of the relative percent error:
It is evaluated only when there is an independent determination that is accepted as the true
value.
In those cases where the true value is not known it is possible to substitute for the "true" value
the
mean of the replicate determinations in order to calculate the relative percent error.
Precision of a measurement refers to the reproducibility of the results, i.e. the
agreement between
values in replicated trials. Chemical analyses are usually performed in triplicate. It is unsafe to
use
only two trials because in case of a deviation one has no idea which of the two values is more
reliable. It is generally too laborious to use more than three samples.
AVERAGE DEVIATION
The precision of a set of measurements is usually expressed in terms of the standard
deviation.
A
somewhat easier to understand and for small data sets just as meaningful measure of precision is
the
average deviation. The steps required to calculate this average deviation are
summarized below.
1. Calculate the arithmetic mean (average) of the data set.
2. Calculate the deviation of each determination from the mean.
3. Now calculate the sum of the absolute values of the deviations found in 2. above. Then
divide this sum by the number of determinations.
The result of the analysis can then be expressed as the "mean + average deviation".
This procedure may be illustrated with the following data. Assume that you wanted to calculate the average mileage per gallon of gasoline of your car. Results of three different trials carried out under similar driving conditions gave the following miles per gallon:
20.8, 20.4 and 21.2
The arithmetic mean can be calculated as (20.8 + 20.4 + 21.2)/3=20.8
The Deviation from the Mean in each case is
|20.8-20.8|=0.0
|20.4-20.8|=0.4
|21.2-20.8|=0.4
The average deviation from the mean is then calculated as
(0.0+0.4+0.4)/3=0.3, to one
significant figure
Therefore, the experimental value should be reported as:
REJECTION OF DATA
When a set of data contains an outlying result that appears to deviate excessively from the
average or
median, the decision must be made to either retain or reject this particular measurement. The
rejection of a piece of data is a serious matter which should never be made on anything but the
most
objective criteria available, certainly never on the basis of hunches or personal prejudice. Even a
choice of criteria for the rejection of a suspected result has its perils. If one demands
overwhelming
odds in favor of rejection and thereby makes it difficult ever to reject a questionable
measurement,
one runs the risk of retaining results that are spurious. On the other hand, if an unrealistically
high
estimate of the precision of a set of measurements is assumed a valuable result might be
discarded.
Most unfortunately, there is no simple rule to give one guidance. The Q-Test has some
usefulness if
there is a single measurement which one suspects might deviate inordinately from the rest of the
measurements:
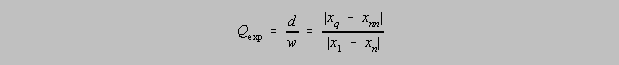 In a set of n
measurements if one observes a questionable value (an outlier), xq, the absolute
value of
the difference between that value and its nearest neighbor, xnn , divided by the
absolute value of
difference between the highest and lowest value in the set is the experimental quotient Q, or
Qexp . If
Qexp exceeds a given "critical" Q (Qcrit) for a given level of
confidence then one might decide to reject
that value at the given level of confidence. A table(1) of
values of Qcrit is given below:
In a set of n
measurements if one observes a questionable value (an outlier), xq, the absolute
value of
the difference between that value and its nearest neighbor, xnn , divided by the
absolute value of
difference between the highest and lowest value in the set is the experimental quotient Q, or
Qexp . If
Qexp exceeds a given "critical" Q (Qcrit) for a given level of
confidence then one might decide to reject
that value at the given level of confidence. A table(1) of
values of Qcrit is given below:
| n (observations) | 90% conf. | 95% conf. | 99% conf. |
| 3 | .941 | .970 | .994 |
| 4 | .765 | .829 | .926 |
| 5 | .642 | .710 | .821 |
| 6 | .560 | .625 | .740 |
| 7 | .507 | .568 | .680 |
| 8 | .468 | .526 | .634 |
| 9 | .437 | .493 | .598 |
| 10 | .412 | .466 | .568 |
GENERAL OBSERVATIONS ON OUTLYING RESULTS
In light of the foregoing, a number of recommendations, for the treatment of data sets
containing a
suspect result, can be made.
1. Estimate the precision that can reasonably be expected from the method. Be certain
that
the
outlying result is indeed questionable.
2. Re-examine carefully all data relating to the questionable result in order to rule out the
possibility that a gross error has affected its value. Remember that the only sure justification for
rejection is the knowledge of a gross error.
3. Repeat the analysis, if at all possible. Agreement of the newly acquired value with
those
that
appear to be valid will support the contention that the outlying result should be rejected.
4. If further data cannot be obtained apply the Q-Test. Also give consideration to reporting the median, rather than the mean value of the set. The median is the central value of the set and it will minimize the influence of the outlying result.