Chapter 3. Gravimetry

Gravimetric methods of analysis are used where weights of reactants and products of chemical reactions are reproducible, stable and reflect the presence of constituents which are important in the establishment of identity.

Two important methods deal with the trapping and weighing of products in the solid and gaseous phases. The first of these falls into the category of a precipitation method.

3-1. Precipitation methods. Many metallic elements in their ionic forms react with negative counter ions to produce stable precipitates. Silver ions form stable and highly insoluble salts with chloride, bromide and iodide. Calcium precipitates quantitatively with oxalate and can be measured reproducibly at any of three temperature dependent plateaus as the oxalate, the carbonate and the oxide. Barium precipitates quantitatively as the sulfate. The reactions often follow the same patterns:

Positive and negative ions in an aqueous solution, otherwise soluble with the counter ions in their environment, produce highly insoluble precipitates with certain added reagents.

3-2. Volatilization methods. An interesting volatilization method which is entirely gravimetric is the one shown by the equations below.

The analyte can be bicarbonate as shown or a mixture of carbonate and bicarbonate. The total amount of carbonate in whatever form is found by placing the analyte in a solution containing an excess of H₂SO₄. This solution is in a flask connected to incoming nitrogen gas gently bubbled through the solution and an exit tube first to a drying agent to absorb aerosolized water and water vapor and then to a mixture of NaOH and drying agent to absorb the CO₂ and

water subsequently produced by the absorption by NaOH:

The apparatus is shown below. The tube containing the NaOH on asbestos and the CaSO₄ to absorb the final water product is pre- and post-weighed to given the total amount of carbonate in the sample. Note that the nitrogen gas acts only as a carrier and does not take part in any reaction.

Precipitates ought to be easy to wash free of contaminants without loss of the precipitate either in solution or through the filter. The particle size of the precipitate ought to be large enough not to escape through the filter pores. That the precipitate has a low solubility is paramount. The precipitate ought not to react with the atmosphere and it must have a known composition which remains stable after ignition.

3-3a. Substances of low solubility have the nasty habit of forming colloidal suspensions. Colloidal particles have diameters from 10^-7 cm to 10^-4 cm. That is on the order of from 10 atomic diameters to 10,000 atomic diameters. Particles in this size range are still sufficiently jostled about by thermal molecular motion to remain in suspension. Where they are the result of a process of precipitation brought about by the addition of ionic species, the particles are surrounded by the excess ionic species. If Ba²⁺ is added in excess to SO₄^2- the BaSO₄ precipitate which is formed is considered to be surrounded by Ba²⁺ ions. If the opposite procedure were being followed, the precipitate would be surrounded by SO₄^2- ions. That these particles all have like charge and therefore repel each other suggests that your technique must favor the formation of large rather than small precipitate particles and to offer ways of encouraging the coagulation of particles after they have formed.

This can be done by carrying out the precipitation at a temperature close to the boiling point of water, in a dilute solution of your analyte and with constant stirring for the reasons given below.

Although analytical chemists still have some disagreement as to the mechanism of precipitation, there is wide agreement that a quantity called the relative supersaturation affects the particle size. Relative supersaturation is given as

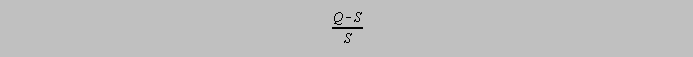
where Q is the instantaneous concentration of the species added to effect precipitation and S is the equilibrium solubility of the substance which precipitates. Particle size seems to be inversely proportional to Relative Supersaturation because a high concentration of added reagent increases the probability that oppositely charged ions will begin the precipitation process at late as well as early stages of the addition and the resulting particles will be on the order of atomic dimensions, whereas the maintenance of a value of Q just slightly above S lowers that probability but offers in any case a layer of the added reagent ions around existing particles for their further growth.

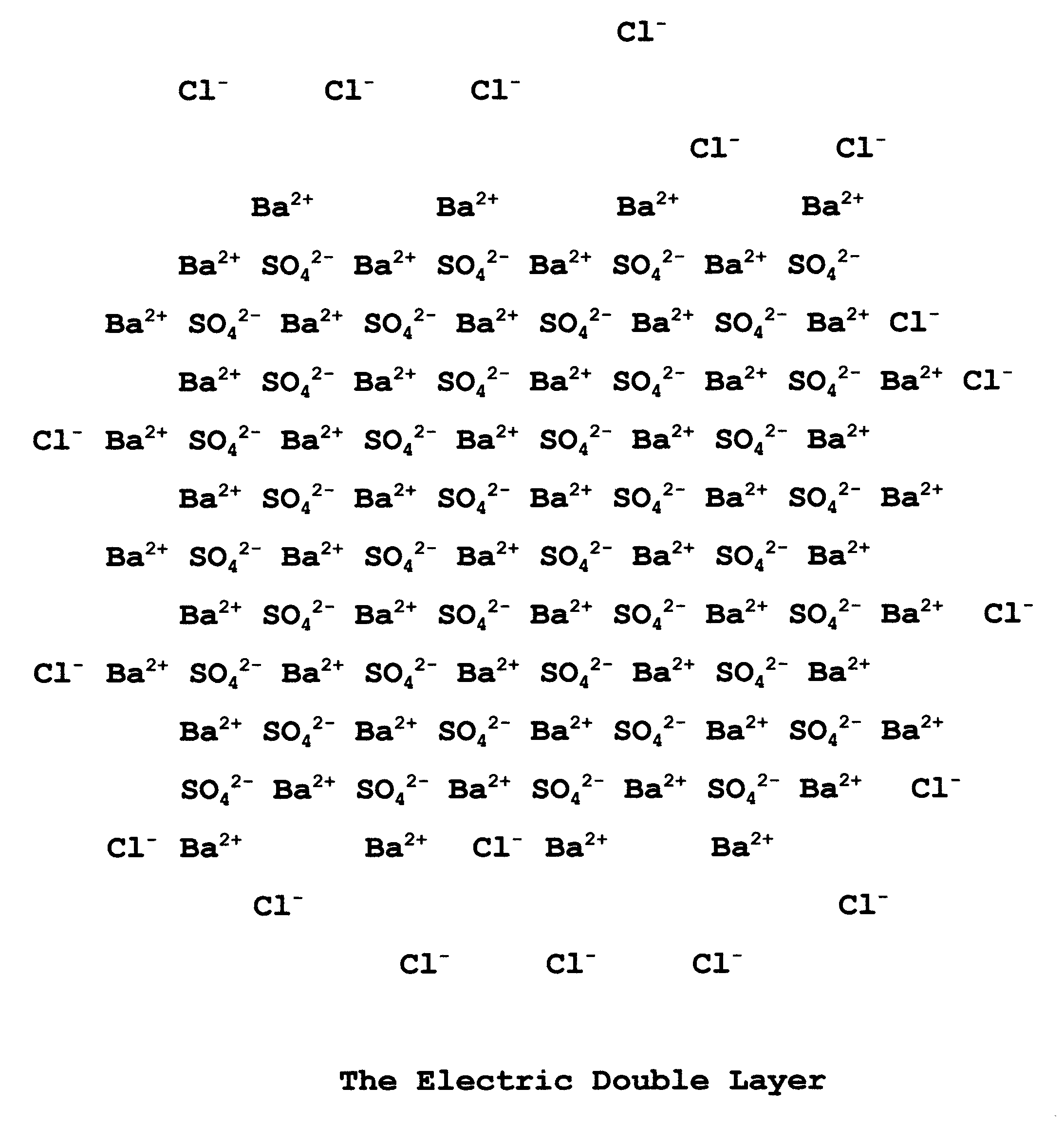
If a particle of precipitate is surrounded by the ion in excess, say Ba²⁺ in the case of the determination of SO₄^2-, any negative ions in the immediate surroundings will be attracted to that primary positive layer. In the case of the addition of a BaCl₂ solution to a Na₂SO₄ solution, the ions Cl^- and SO₄^2- are available. As the sulfate is used up in the precipitation process it is the chloride which is left and which forms the second layer. Thus we have an electric double layer, made up first of barium ions then of chloride ions. This double layer keeps the colloidal precipitate particles from coming into contact with each other for further coagulation.

There are two ways to bring the particles closer together and to increase the probability of coagulation: (1) heating increases overall thermal motion, affecting both the mobility of adsorbed ions and of the colloidal precipitate particles themselves. The summary effect is that there are collisions of particles which result in the increase in particle size due to increased coagulation; (2) increasing the electrolyte concentration of the solution, for reasons not entirely clear, results in a decrease in the mean radius of the electric double layer and encourages further coagulation. Carrying out both of these operations results in digestion of the precipitate, an unfortunate term because biological digestion usually refers to the dissolving of food and absorption at the molecular level through the wall of the intestine. Digestion in quantitative analysis refers to the coagulation of a precipitate into a filterable form. Unfortunately after successful digestion, some of the primary electric layer is made up of Na⁺ ions which must be washed away ultimately for quantitative results to be achieved. The Ba²⁺ ions as well will give a positive error if not removed and end up being dried with the precipitate as excess BaCl₂. Many coagulated precipitates do not respond well to washing with distilled water because as the second electric layer is removed (excess Cl^- for example) the first remains on all particles with an electric charge of the same sign. The result is that there is a return to the repulsive state and an effective increase in the radius of the particles which then begin once again to separate as colloidal particles. The process is called peptization and is to be avoided if some of the precipitate is not to be lost. One way around this for many precipitates is to encourage digestion by heating and also by increasing the electrolyte concentration by washing with a reagent which will go off as a gas during the drying process. Dilute nitric acid, HNO₃ , is effective for washing excess ions from AgCl. In choosing such a wash, it is imperative that the procedure has been carried out and has been shown to yield reproducible, quantitative results. Unexpected side reactions, complex formation and changes in solubility with added reagents are sufficiently unpredictable to make intuition in the absence of experience unacceptable.

During the precipitation procedure a number of other problems can arise to give erroneous positive or negative results. Among these are surface adsorption, mixed crystal formation, occlusion and mechanical entrapment.

Any ions may be carried down during a precipitation as the result of surface adsorption. Na⁺ , or Cl^- in the case of the determination of SO₄^2- by the addition of dilute BaCl₂ solution to a NaSO₄ solution. Both Ba²⁺ and Na⁺ can compete for lattice positions as the particles form. Likewise, the ions Cl^- and SO₄^2- can have the same effect. In the quantitative determination of some transition metals, iron for example as Fe(OH)₃, zinc, cadmium and manganese may be present as impurities and all three form sparingly soluble hydroxides as well, though each with greater solubility than the hydroxide of iron:

Compound	Solubility Product
Fe(OH)₃	4 x 10^-38
Cd(OH)₂	2.5 x 10^-14
Mn(OH)₂	1.9 x 10^-9
Zn(OH)₂	1.2 x 10^-17

Mixed crystal formation can occur if two ions have the same charge, if their ionic diameters are sufficiently close to fit into the same crystal lattice. Ions which commonly interfere with each other are shown in the table below with their ionic diameters in picometers given after each.

Interfering	Ions
K⁺, 133 pm	NH₄⁺, 148 pm
Sr²⁺, 113 pm	Ba²⁺, 135 pm
Mn²⁺, 80 pm	Cd²⁺, 97 pm

In cases where one has a known interference of one ion with the other it is necessary to find methods of removing one before carrying out a precipitation of the other, or using a precipitating reagent in which there is no interference.

Occlusion and mechanical entrapment. If a precipitation procedure is carried out too quickly, pockets of solvent and spectator ions can form, trapping them within the precipitate particles and dashing one's hope of removing them during the washing procedure. This is another reason why the relative supersaturation must be kept as low as possible so that in principle at least, all precipitation occurs only at the surface of a growing solid particle, devoid of solvent pockets.

All of these problems of coprecipitation of unwanted ions can lead to positive or negative errors. In the example above where it pointed out that Na⁺ or Cl^- may coprecipitate in the SO₄^2- determination, surface adsorption will produce a positive error. In the case of mixed crystal formation, the direction of the error depends on the relative atomic weight of the ion which replaces that which is desired in the precipitate. In the case of the precipitation of zinc hydroxide, mixed crystal formation with manganese would produce a negative error but with cadmium or zinc a positive error.

		Desired precipitate
Compound	Mn(OH)₂	Zn(OH)₂	Cd(OH)₂
At. Wt. of M²⁺	54.94	65.39	112.41
Direction of error	negative	---	positive

A solution containing a reagent which produces a desired ion to effect precipitation, often by gentle heating of the solution, offers an exquisite means for obtaining well-formed large crystal particles which lend themselves splendidly to the technique of filtration.

The model we use to explain why this happens also uses the concept of relative supersaturation. The initial nucleation of sparingly soluble particles offers a surface template which favors "locking" onto ions in the vicinity which by the luck of the draw (and the kinetic molecular theory) find themselves at the right energy and orientation to enter the crystal lattice. Ions isolated from a growing crystal are not favored to enter this process because at least two are required, both at the right energy and orientation to start the growth of a new crystal. If the concentration of one ion of a sparingly soluble salt increases gradually by slow homogeneous synthesis in a solution, then as its concentration reaches the threshold of supersaturation for the ion pair, a relatively small number of nucleated particles grows to larger size (because the probability of finding a place in an existing crystal lattice for any single ion is greater than that of a spontaneous creation a new crystal from dissolved and randomly arranged ions) rather than a large number of nucleated particles growing in constant competition with the rest and thus remaining small. The result for the latter is a non-filterable precipitate, but one in the former which filters quite well.

Here is a table of common reagents useful for the preparation of ions often needed for precipitation processes.

Reagent	Precipitating species	Precipitation reaction	Elements which yield to this reaction
Urea	OH^-	(NH₂)₂CO + 3H₂O ---> CO₂ + 2NH₄⁺ + 2OH^-	Al, Ga, Th, Bi, Fe, Sn
Trimethyl phosphate	PO₄^3-	(CH₃O)₃PO + 3H₂O ---> 3CH₃OH + H₃PO₄	Zr, Hf
Ethyl oxalate	C₂O₄^2-	(C₂H₅)₂C₂O₄+ 2H₂O ---> 2C₂H₅OH + H₂C₂O₄	Mg, Zn, Ca
Dimethyl sulfate	SO₄^2-	(CH₃O)₂SO₂+ 4H₂O ---> 2CH₃OH +SO₄^2- + 2H₃O⁺	Ba, Ca, Sr, Pb
Trichloroacetic acid	CO₃^2-	Cl₃CCOOH + 2OH^- ---> CHCl₃ + CO₃^2- + H₂O	La, Ba, Ra
Thioacetamide	H₂S	CH₃CSNH₂ + H₂O ---> CH₃CONH₂ + H₂S	Sb, Mo, Cu, Cd
Dimethyl glyoxime	CH₃(CNOH)₂CH₃	CH₃COCOCH₃ + 2H₂NOH ---> DMG + 2H₂O	Ni
8-Acetoxyquinoline	C₉H₆NOH	CH₃COOQ + H₂O ---> CH₃COOH + HOQ	Al, U, Mg, Zn

The resulting precipitate must be heated until a stable dry state is reached. Some understanding of typical precipitate properties is mandatory for repeatable results to be achieved.

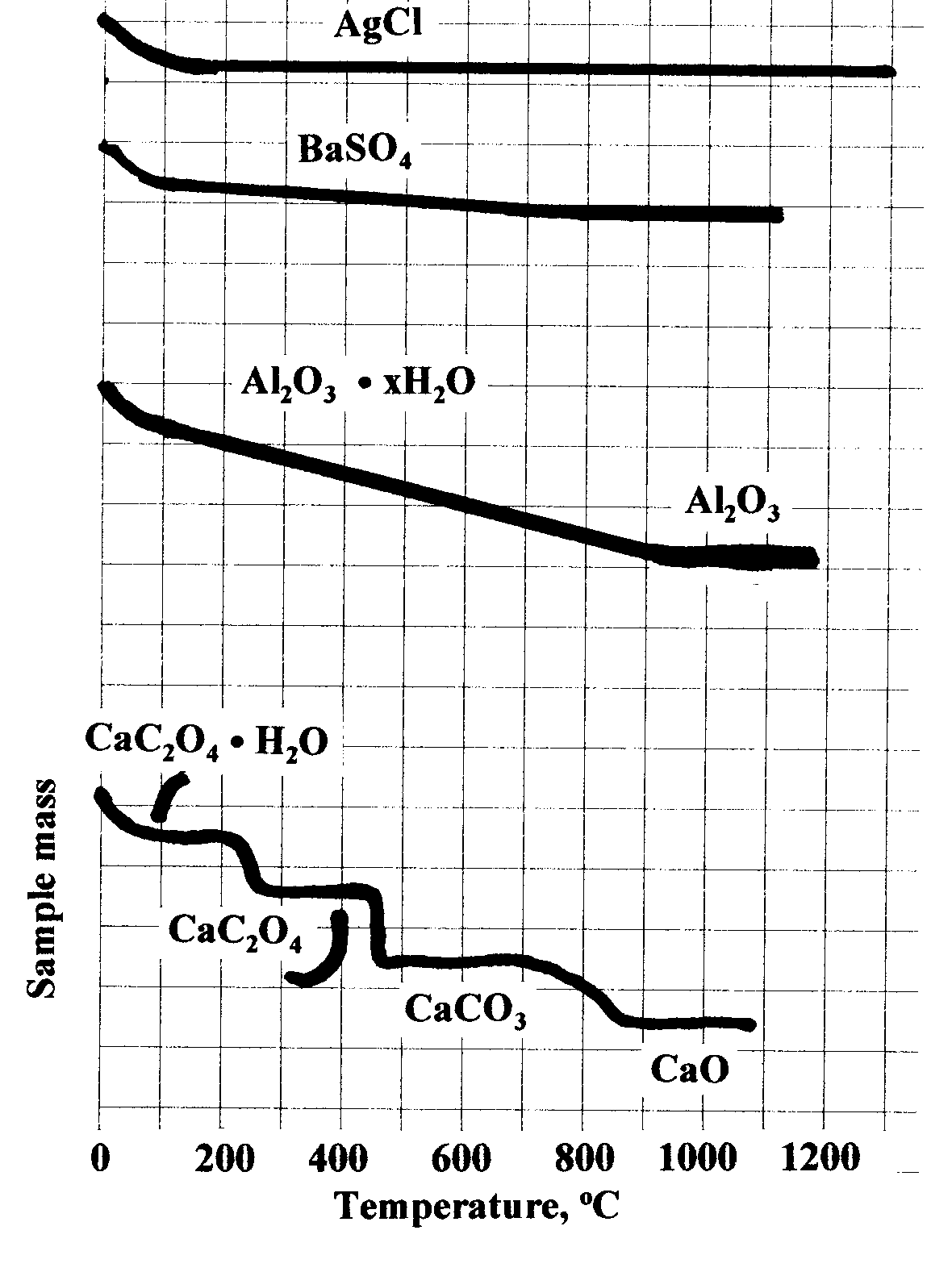Note in the figure at the right that whereas AgCl achieves a stable dry weight just above 100^oC, BaSO₄ does not do so until it reaches a temperature in the vicinity of 700^oC Aluminum oxide, Al₂O₃, loses water slowly as the temperature rises to 1000^oC at which point it achieves stability. Some compounds decompose in several stages, reaching stable plateaus. Calcium oxalate, CaC₂O₄ H₂O, loses all its water at around 200^oC and remains stable as CaC₂O₄ until just above 400^oC at which point it decomposes to calcium carbonate, CaCO₃ where it remains stable up to 700^oC. Between 700^oC and 850^oC it slowly decomposes to CaO where it remains stable until its melting point at 2614^oC.

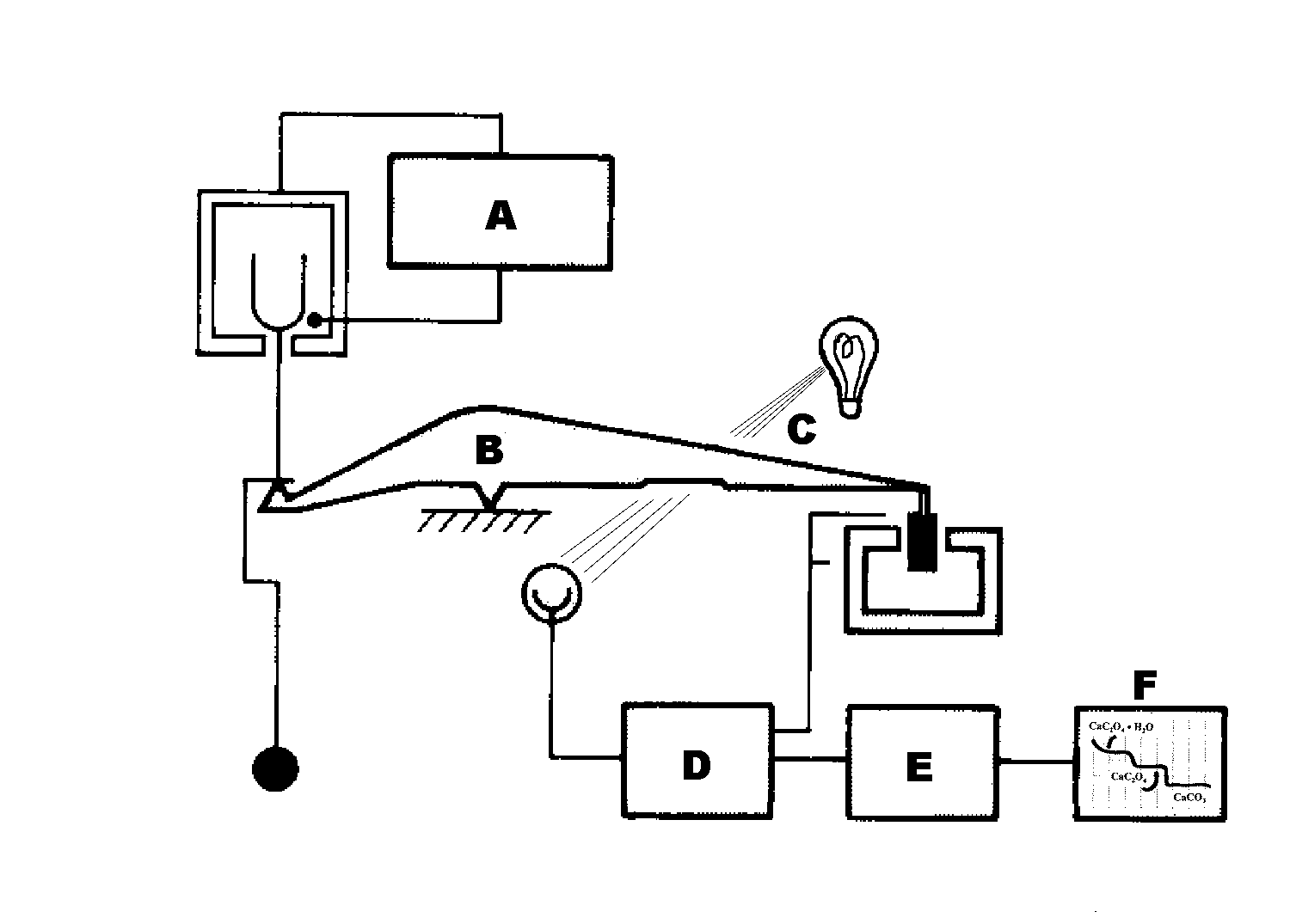
A device not seen often in analytical laboratories but useful for producing automatic plots of mass of sample vs. temperature such as those at the right is the thermobalance (below). Region A includes the heating circuit, a temperature sensor, sample cup and counter weight resting on one end of the balance arm, B. A light wave is partially attenuated at C, giving a negative feedback to the amplifier circuit at D, designed to yield an output voltage which increases with the force necessary to keep the balance in equilibrium (and the attenuation at a constant value). One can adjust the baseline voltage at E, the tare adjuster, so as to produce the graph at the chart recorder, F.

Example 3-1: A 0.3427 g sample of bronze-age jewelry is analyzed for silver content by first dissolving it in concentrated nitric acid and precipitating it as AgCl. The precipitate is transferred to a dry sintered glass filter weighing 12.2347 g where it is separated from the filtrate and washed with dilute nitric acid. The filter and precipitate are dried at 150^oC, cooled, weighed and found to weigh 12.4373 g. Calculate the %Ag in the jewelry.

Example 3-2. A sample of iron ore weighing 0.4275 g is dissolved in 12M HCl. The resulting solution is slowly made basic with NaOH until the first hint of a turbid solution is detected. 10.0 g urea are dissolved and the solution heated just to the boiling point for 4 hours. The precipitate, Fe₂O₃ x H₂O, is trapped using ashless filter paper. The precipitate and filter paper are fired in a porcelain crucible of empty weight 12.2837g until the ashless filter paper is completely incinerated and anhydrous Fe₂O₃ is left. The resulting weight of crucible and precipitate is 12.4274 g. Determine the %Fe, the %Fe₂O₃ and the %Fe₃O₄.

Example 3-3. A sample known to contain only KCl and NaCl and weighing 0.4263 g is dissolved in water and treated to an excess of AgNO₃, using standard methods of precipitation. The AgCl precipitate is caught on a Gooch Crucible of original dry weight of 15.2748 g. The AgCl precipitate is dried at 150^oC, cooled and the crucible and precipitate are found to weigh 16.2872 g. Determine the %KCl and the %NaCl in this sample.

Solution is based on the difference in the %Cl in the pure salts:

Salt	%Cl
NaCl	60.66
KCl	47.55

3-8. Preferred methods of gravimetric analysis. Most inorganic ions have yielded to gravimetric analytical techniques, but one finds many interfering ions. The table below illustrates both the abundance of reagents available for use as well as the problems which can be encountered by interfering ions:

Analyte	Precipitate	Measured form	Interferences
K⁺	KB(C₆H₅)₄	KB(C₆H₅)₄	NH₄⁺,Ag⁺,Hg²⁺, Tl⁺,Rb⁺,Cs⁺
Mg²⁺	Mg(NH₄)PO₄.6H₂O	Mg₂P₂O₇	Many metals (none from Na⁺ and K⁺)
Ca²⁺	CaC₂O₄.H₂O	CaCO₃ or CaO	Many metals (none from Mg²⁺, Na⁺ and K⁺)
Ba²⁺	BaSO₄	BaSO₄	Na⁺,K⁺,Li⁺,Ca²⁺,Al^3 +,Cr³⁺,Fe³⁺,Sr²⁺,Pb²⁺
Ti⁴⁺	TiO(5,7-dibromo-8-hydroxyquinoline)₂	TiO(5,7-dibromo-8-hydroxyquinoline)₂	Fe³⁺,Zr⁴⁺,Cu²⁺,C₂O₄^2-, citrate, HF
VO₄^3-	Hg₃VO₄	V₂O₅	Cl^-,Br^-,I^-,SO₄^2- , CrO₄^2-,AsO₄^3-,PO₄^3-< / sup>
Cr³⁺	PbCrO₄	PbCrO₄	NH₄⁺,Ag⁺
Mn²⁺	Mn(NH₄)PO₄.H₂O	Mn₂P₂O₇	Interferences from numerous metals
Fe³⁺	Fe(HCO₂)₃	Fe₂O₃	Interferences from numerous metals
Co²⁺	Co(1-nitroso-2-naphtholate)₃	CoSO₄ (by reaction with H₂SO₄ )	Fe³⁺,Zr⁴⁺,Pd²⁺
Ni²⁺	Ni(dimethylglyoximate)₂	Ni(dimethylglyoximate)₂	Pd²⁺,Pt²⁺,Bi³⁺,Au³⁺
Cu²⁺	CuSCN	CuSCN	NH₄⁺,Pb²⁺,Hg²⁺,Ag⁺
Zn²⁺	Zn(NH₄)PO₄.H₂O	Zn₂P₂O₇	Interferences from numerous metals
Ce⁴⁺	Ce(IO₃)₄	CeO₂	Th⁴⁺,Ti⁴⁺,Zr⁴⁺
Al³⁺	Al(8-hydroxyquinolate)₃	Al(8-hydroxyquinolate)₃	Interferences from numerous metals
Sn⁴⁺	Sn(cupferron)₄	SnO₂	Cu²⁺,Pb²⁺,As(III)
Pb²⁺	PbSO₄	PbSO₄	Ca²⁺,Sr²⁺,Ba²⁺,Hg²⁺, Ag⁺,HCl, HNO₃
NH₄⁺	NH₄B(C₆H₅)₄	NH₄B(C₆H₅)₄	K⁺, Rb⁺, Cs⁺
Cl^-	AgCl	AgCl	Br^-, I^-, SCN^-, S^2-, S₂O₃^2-, CN^-
Br^-	AgBr	AgBr	Cl^-, I^-, SCN^-, S^2-, S₂O₃^2-, CN^-
I^-	AgI	AgI	Br^-, Cl^-, SCN^-, S^2-, S₂O₃^2-, CN^-
SCN^-	CuSCN	CuSCN	NH₄⁺,Pb²⁺,Hg²⁺,Ag⁺
CN^-	AgCN	AgCN	Cl^-, Br^-, I^- , SCN^-, S^2-, S₂O₃^2-
F^-	(C₆H₅)₃SnF	(C₆H₅)₃SnF	Except alkali metals, many interferences, and SiO₄^4- , CO₃^2-
ClO₄^-	KClO₄	KClO₄
SO₄^2-	BaSO₄	BaSO₄	Na⁺,K⁺,Li⁺,Ca²⁺,Al^3 +,Cr³⁺,Fe³⁺,Sr²⁺,Pb²⁺
PO₄^3-	Mg(NH₄)PO₄.6H₂O	Mg₂P₂O₇	Many interferences except Na⁺,K⁺
NO₃^-	Nitron nitrate	Nitron nitrate	ClO₄^-, I^-, SCN^-, CrO₄^2-,ClO₃^-, NO₂^-, Br^-, C₂O₄^2-
CO₃^2-	CO₂ (by addition of acid)	CO₂	CO₂ is trapped as Na₂CO3 on Ascarite

There are a number of organic functional groups which precipitate with metal ions by one of two routes: (1) chelating agents are organic compounds which "wrap around" a metal ion thanks to cationic side chains which form coordinate covalent bonds with the ion, and (2) a straightforward ion-ion bond which produces a new species that excludes water of solvation and thus precipitates. Good examples of chelating agents include Ethylene Diamine Tetraacetic Acid (EDTA), oxalic acid, glycine, 8-hydroxyquinoline and dimethylglyoxime.

Some common organic precipitating agents:

Compound	Ions precipitated
Dimethylglyoxime	Ni²⁺,Pd²⁺,Pt²⁺
EDTA (Ethylenediamine tetraacetic acid)	Zn²⁺, Cu²⁺, Pb²⁺, Ca²⁺, Ni²⁺, Fe³⁺
Cupferron	Fe³⁺,VO₂⁺,Ti⁴⁺, Zr⁴⁺,Ce⁴⁺,Ga³⁺,Sn⁴⁺
8-Hydroxyquinoline	Fe³⁺,Al³⁺,Mg²⁺,Zn²⁺, Cu²⁺,Cd²⁺,Pb²⁺, Bi³⁺, Ga³⁺,Th⁴⁺, Zr⁴⁺, TiO²⁺, UO₂²⁺
Salicylaldoxime	Bi³⁺,Ni²⁺,Pd²⁺,Zn²⁺, Cu²⁺,Pb²⁺
1-Nitroso-2-naphthol	Fe³⁺,Co²⁺,Pd²⁺, Zr⁴⁺
Nitron (C₂₀H₁₆N₄)	NO₃^-, ClO₄^-, BF₄^-, WO₄^2-
Sodium tetraphenylborate	NH₄⁺, organic ammonium, Ag⁺, Cs⁺, Rb⁺, K⁺
Tetraphenylarsonium chloride	Cr₂O₇^2-, MnO₄^-, ReO₄^-, MoO₄^2-,WO₄^2-, ClO₄^-

Disclaimer: The views and opinions expressed on unofficial pages of California State University, Dominguez Hills faculty, staff or students are strictly those of the page authors. The content of these pages has not been reviewed or approved by California State University, Dominguez Hills.