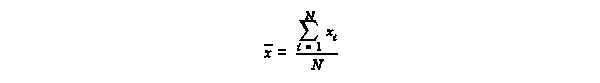
Chapter 5. Errors in chemical analysis
Any measurement is limited by the precision of the measuring instruments and the technique
and
the skill of the observer. Where a measurement consists of a single reading on a simple piece of
laboratory equipment, for example a burette or a thermometer, one would expect the number of
variables contributing to uncertainties in that measurement to be fewer than a measurement
which
is the result of a multi-step process consisting of two or more weight measurements, a titration
and the use of a variety of reagents.
It is important to be able to estimate the uncertainty in any measurement because not doing
so
leaves the investigator as ignorant as though there were no measurement at all. The phrase "not
doing so" perpetuates the myth that somehow a person can make a measurement and not know
anything about the variability of the measurement. That doesn't happen very often. A needle
swings back and forth or a digital output shows a slight instability, so the investigator can
estimate
the uncertainty, but what if a gross error is made in judgment, leading one to estimate an
unrealistic "safe" envelope of uncertainty in the measurement? Consider the anecdote offered by
Richard Feynman about one of his experiences while working on the Manhattan Project during
World War II. Although this example doesn't address
the uncertainty of a particular measurement it touches on problems which can arise when there is
complete ignorance of parameter boundaries:
Some of the special problems I had at Los Alamos were rather interesting. One thing had to do with the safety of the plant at Oak Ridge, Tennessee. Los Alamos was going to make the [atomic] bomb, but at Oak Ridge they were trying to separate the isotopes of uranium -- uranium 238 and uranium 235, the explosive one. They were just beginning to get infinitesimal amounts from an experimental thing [isotope separation] of 235, and at the same time they were practicing the chemistry. There was going to be a big plant, they were going to have vats of the stuff, and then they were going to take the purified stuff and repurify and get it ready for the next stage. (You have to purify it in several stages.) So they were practicing on the one hand, and they were just getting a little bit of U235 from one of the pieces of apparatus experimentally on the other hand. And they were trying to learn how to assay it, to determine how much uranium 235 there is in it. Though we would send them instructions, they never got it right.
So finally Emil Segrè said that the only possible way to get it right was for him to go down there and see what they were doing. The army people said, "No, it is our policy to keep all the information of Los Alamos at one place."
The people in Oak Ridge didn't know any thing about what it was to be used for (that is, they didn't have knowledge of its range of safety -- O.S.); they just knew what they were trying to do. I mean the higher people knew they were separating uranium, but they didn't know how powerful the bomb was, or exactly how it worked or anything. The people underneath didn't know at all what they were doing. And the army wanted to keep it that way. There was no information going back and forth. But Segrè insisted they'd never get the assays right, and the whole thing would go up in smoke. So he finally went down to see what they were doing, and as he was walking through he saw them wheeling a tank carboy of water, green water -- which is uranium nitrate solution.
He said, "Uh, you're going to handle it like that when it's purified too? Is that what you're going to do?"
They said, "sure -- why not?"
"Won't it explode?" he said.
Huh! Explode?
Then the army said, "You see! We shouldn't have let any information get to them! Now they are all upset."
It turned out that the army had realized how much stuff we needed to make
a bomb -- twenty kilograms or whatever it was -- and they realized that this much
material, purified, would never be in the plant, so there was no danger. But they
did not know that the neutrons were enormously more effective when they are
slowed down in water. In water it takes less than a tenth -- no, a hundredth -- as
much material to make a reaction that makes radioactivity. It kills people around
and so on. It was very dangerous, and they had not paid any attention to the safety
at all.(1)
Feynman's example illustrates that although there were individuals who knew something
about
the boundary of parameters in which one could safely work with these materials in the solid state,
both they and the people who were doing the work had no knowledge of the parameters or
boundaries of safety for the conditions under which the work was being done (in aqueous
solution). That ignorance rendered their knowledge useless. That the nuclear accident in Japan
in
1999 came about because of the ignorance of this same characteristic of
neutrons after having
been documented in many lay accounts of the history of nuclear energy testifies to the continuing
illusion over the "justification of secrecy" even in the face of imminent danger to workers,
equipment and the population at large.
A second recent case of knowledge rendered useless without recognizing the presence of a
fatal
uncertainty involved the loss of the Mars Climate Orbiter on September 23, 1999. As reported in
the L.A. Times, "the $125 million spacecraft was lost because NASA navigators mistakenly
thought a contractor used metric measurements. The contractor had used English units, and the
probe burned up in the Martian atmosphere Sept. 23."
Information is useless if there is no knowledge of the precision of that information. Such
uselessness may be the result of
1) the presentation of a single number as a statement of the information, but lacking an estimated error.
2) gross error in calculation or data collection.
A gross error is not necessarily one in which the investigator fails to report a precision if it is known which equipment was used, say an analytical balance with a precision of ±0.0001 g or a 50 mL buret with a precision of ±0.01 mL. Data presented to a number of significant figures less than that justifiable by the equipment certainly demonstrates carelessness but doesn't, in this writer's opinion, rise to the level demonstrated by a student doing a titration using the wrong solution, NASA engineers effecting a mid-course maneuver of a deep space probe based on the wrong system of units or Oak Ridge technicians carrying out purification procedures of 235U thinking that their margin of safety is 100 times greater than it is. The latter examples illustrate the very dangerous situation of investigators not knowing what they think they know, that is, some window of confidence in their data. That's when the data become useless.
Another and shorter way of saying the same thing is that without some knowledge of the
uncertainty of a measurement, the reported value could be anything. A piece of jewelry could
have a weight % gold of 0% or 100%. It wouldn't matter what one were to report if there is no
knowledge of the experimental uncertainty.
Once experimental uncertainty is revealed, it is a forewarning of the boundaries beyond
which
there may be no experimental confidence. Without that knowledge all bets are off. The
engineers
of the Mars Climate Orbiter didn't have any boundaries beyond
which lay potential disaster. The
disaster was everywhere and nowhere. They were reduced to crossing their fingers as a Plan A
for saving the mission. Science ought not to work that way. With the knowledge of
experimental
uncertainty intelligent decisions which were impossible before can be made.
In this chapter the important concepts of precision and accuracy will
be introduced. Moreover,
we will be concerned with the spread or range of a series of readings,
and
of decisions connected
with removing outliers from a data set. The median and arithmetic
mean will be discussed in the
context of reporting a best value from a data set exhibiting random errors. Our
discussion of
accuracy as regards the closeness of a reported result to some true value
and how precision and
accuracy may differ due to systematic errors will be discussed.
Often an analytical chemist is faced with a choice between time constraints and accuracy;
hence
the question of maximum error tolerance must be asked. The determination of quantities of
DNA
sequences in a forensic lab may rest heavily on the "quick and dirty" comparison of intensities of
"blips" of unknown concentrations on an electrophoresis gel with those of known concentrations.
On the other hand, the establishment of conspiracy in a murder case might rest on careful
analysis
of trace elements in a series of bullets fired from different guns to show if they came from the
same batch.
The Shroud of Turin is a celebrated case of time being available to develop adequate means
of
analysis to establish the necessary values beyond reasonable doubt. There was no deadline to be
met before some decision had to be made. Some people claimed that the Shroud had been used
to wrap the body of Jesus, the prophet of Christianity, after his crucifixion, though no one
disputed that its history was not known before the 12th century, when it had become the property
of the cathedral at Turin, Italy. It was not an official Relic of the Church, but its reputation over
the centuries had grown and it probably was responsible for many pilgrimages to the cathedral
among the faithful. When radiocarbon dating was proposed as a way to determine its age, the
proposal was at first rejected because such a sizeable amount of material would have to be used
to
carry out the determination (perhaps as much as 10 cm2 for each sample, and at
least 3 samples
must be taken to assure reproducibility). The fear was that if its age could be traced to the
beginning of the first millennium, then it might well be named a Church Relic -- but one that
would have to be mutilated to gain that stature. So identification of the image had to rest on
non-destructive methods of analysis, such as microscopic observations of the surface. Some said
the
"blood stains" were composed of a common pigment used by 13th century artists,
others claimed
the discoloration to be human blood. Meanwhile, back at the lab, techniques continued to
improve, until reliable radiocarbon dating could finally be done with considerably smaller
samples
(in the case of the shroud, just a few short strands were needed for each sample). Such small
sample sizes were judged by Church authorities not to constitute mutilation and the analysis went
forward. Samples were taken from the shroud and sent to several laboratories along with other
samples of fabrics of known ages. The laboratories were not told which was which. The
reported
values showed close agreement between shroud samples and none suggested an age of the fabric
having been harvested from plants before the 12th century A.D. The committee which had taken
on the task of judging the validity of the analysis was sufficiently satisfied to convince local
Church authorities to retire the claim that it was a Holy Shroud.
Definitions
The arithmetic mean, or
average, is defined as
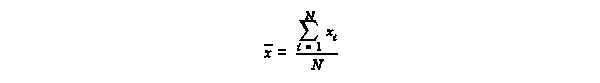
The arithmetic mean is used to report a best value among a series of N replicate
measurements.
The median is the value which divides a set of replicate measurements when the
set is arranged in
order from the smallest to the largest. In the set of titration volumes
23.45, 23.45, 23.47, 23.49, 23.50, 23.51, 23.55,
the arithmetic mean is found by
(23.45 + 23.45 + 23.47 + 23.49 + 23.50 + 23.51 + 23.55)÷7 = 23.489
Since there is uncertainty in the measurements at the hundredths place, it would be best to
report
this value no further. The value 23.49 would suffice except possibly in the rare case where the
set
showed an average deviation or standard deviation somewhat less than ±0.01
The median of this set is 23.49. If there is an even number of readings in the set, the median
is the
mean of the middle pair.
Range or Scatter
Any group of readings may be expected to extend over a range or to show some scatter.
Members of our class are routinely asked to measure the volume reading of water contained in a
burette. The instructor establishes the "true" value in advance by positioning the upper black
boundary of a burette card just under the silhouette of the meniscus. Correct use of a buret is
mandatory if the student is to do well in this class. For some images and instructions on the use
of a buret, go to
http://www.csudh.edu/oliver/demos/buretuse/buretuse.htm
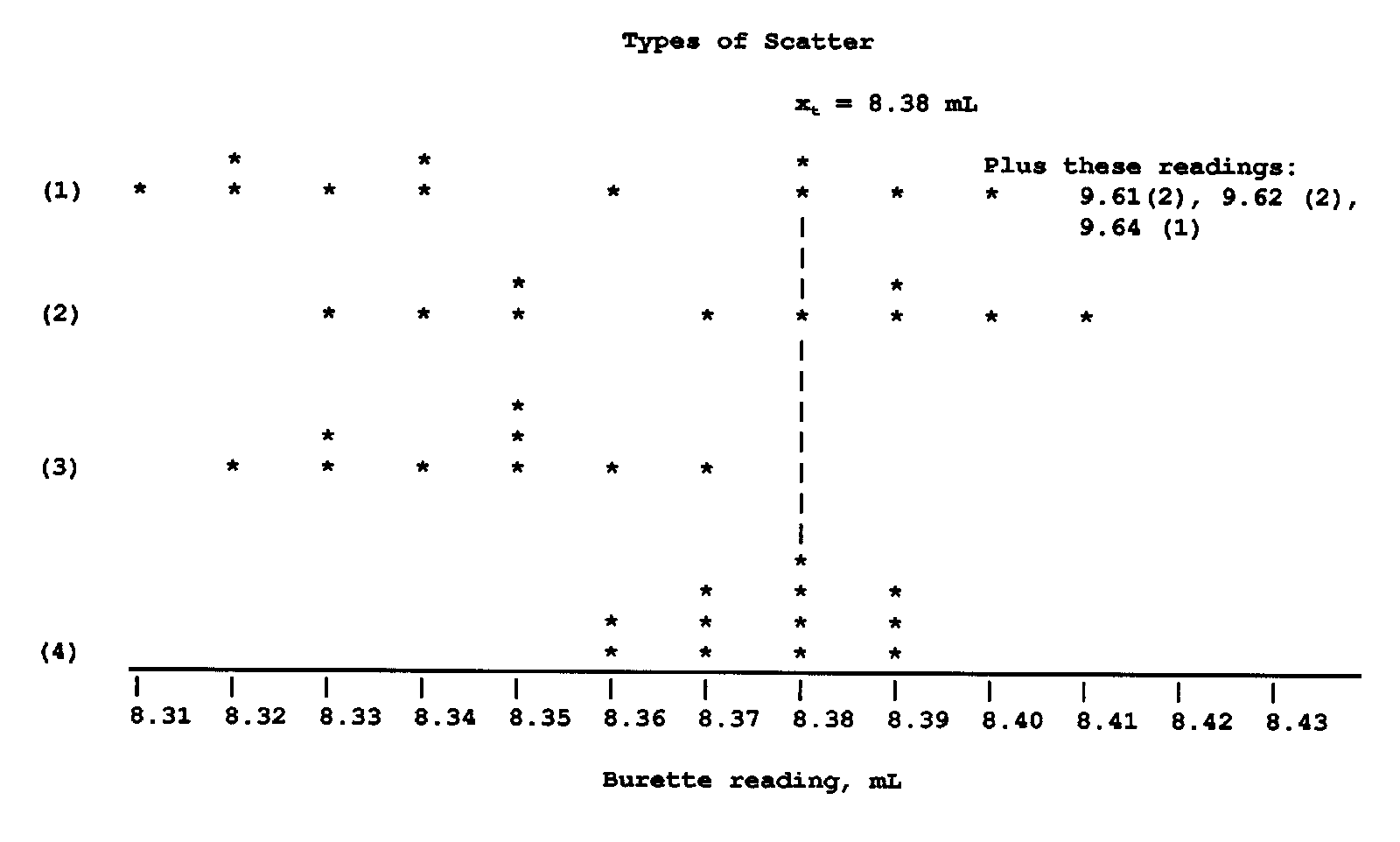 Over the course of a
semester, it is not unusual to observe four types of scatter in student readings
of a burette volume. Scatter is assumed to be the result of random error, influences
caused by
limitations in the equipment used and the limited skill of the observer. There is also the
possibility
of prejudice on the part of the observer and the counterpart to prejudice on the part of the
instrument
used: miscalibration. This second error is referred to as systematic error. The
various types of
scatter one might expect to find among a group of Quantitative Analysis students reading a
burette
are illustrated in the chart at the right.
Over the course of a
semester, it is not unusual to observe four types of scatter in student readings
of a burette volume. Scatter is assumed to be the result of random error, influences
caused by
limitations in the equipment used and the limited skill of the observer. There is also the
possibility
of prejudice on the part of the observer and the counterpart to prejudice on the part of the
instrument
used: miscalibration. This second error is referred to as systematic error. The
various types of
scatter one might expect to find among a group of Quantitative Analysis students reading a
burette
are illustrated in the chart at the right.
(1) Low accuracy and low precision. Note that not only are the readings scattered widely
about the
true value of 8.38 mL, but several students have misconstrued the direction of the scale, reading
upward from the 9.00 mL rather than downward from the 8.00 mL mark. This kind of scatter is
often
observed of student readings at the beginning of the semester. Case (2) which illustrates low
precision and high accuracy. Although this case shows that the
mean
value of all the readings is close to the true value, it could be argued that it is by virtue of luck
more
than anything else that the students arrived at such a good mean value. Case (3) Low accuracy
and
high
precision. Note in the example here that although the readings have a narrower range of scatter
than
in (1) and (2), there seems to be a systematic error in the low direction. If a group of readings are
made without the use of a burette card, the bottom of the meniscus will appear to be higher in the
burette (lower volume) and thus produce such an error. Although burette readings are corrected
by
subtracting the beginning volume from the ending volume, and such systematic errors would tend
to
cancel each other out, a burette card is necessary to produce a common, repeatable background.
Finally, around the 14th week of the semester, students have had enough experience
reading
volumetric scales to present a set of readings like that shown in Case (4), high precision and high
accuracy,
where one sees a narrow range of scatter on both sides of the true value.
Example 5-1. One troy ounce = 31.103486 g. Three students weigh a Krugerand on a
laboratory analytical balance and get
31.1033, 31.1033 and 31.1035 g. What kind of error does this represent, random, systematic or
gross?
Example 5-2. A student weighs a mL of water at 20 oC three times and gets
0.9842, 0.9846 and
0.9844 g. What kind of error does this represent, random, systematic or gross? The density of
water at 20 oC is 0.99823 g/cc.
Example 5-3. A student drops a dry sample of Na2CO3 on the
floor and scoops it up before
titrating it with HCl. What kind of error does this represent, random, systematic or gross?
Precision and accuracy
Precision is a measure of the extent to which the values in a series of readings
vary from the
mean. One speaks of deviations: average deviation and standard
deviation are two expressions
commonly used. The term precision ought not to be used in the context of the agreement of
one's average value with some "true" value. The term to be used in that case is
accuracy, or the
extent to which the mean of a series of readings varies from the "true" value.
The absolute error is the difference between any particular reading
xi and the true value xt:
absolute error = xi - xt
Note that the formula is set up so that a low value produces a negative error and a high value
produces a positive one. Sometimes one speaks of the absolute error of a mean:
![]()
It is often more useful to speak in terms of the relative error which relates the absolute error to
the
value of measurement:
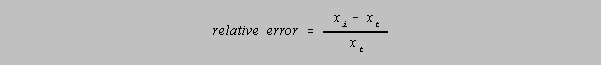
The percent relative error would then be given by
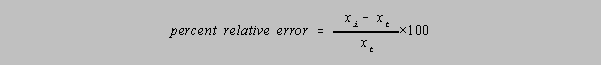
Percent is of course "parts per hundred." It is useful to be able to make conversions between
percent
and parts per thousand (multiply by 10) or even to be able to determine the precision to parts in
some
other number when the other number may be close to some integral power of 10 (100, 1000 or
10000).
Where a number is expressed as 4.372±0.006, the value 0.006 is the "deviation",
"uncertainty" or "precision" expressed in the same units as the measured value, that is, in the
same
context as the absolute error above, the 0.006 would represent an "absolute deviation." or
"absolute precision". So, for 4.372±0.006 g one would estimate an envelope of uncertainty
limited to between 4.366 g and 4.378 g but not greater. One ought to make clear if the 0.006 is
an average deviation or a standard deviation. Relative deviations are then calculated in the same
manner as relative errors above except that the numerator is the absolute deviation by itself. So
the relative deviation or relative precision in parts per thousand of this measured value would be
(0.006/4.372) x 1000 = 1.4 ppt.
Example 5-4. A mixture of magnetite and limestone is found to have 23.72±0.05 % Fe. Determine the relative precision in parts per 100 (percent) and parts per 1000.
(To be solved in class with attention paid to the importance of being able mentally to convert
values
of relative precision to a needed normalization)
Example 5-5. A Chemistry 230 student weighs her last chance (gasp) sample of anhydrous sodium carbonate and finds it to be 0.0842±0.0001 g. How many parts per thousand is her precision and is it good enough to standardize her HCl solution, based on the precision of the equipment we use for this experiment?
(To be solved in class with attention paid to the maximum precision we might expect to
attain
in this
class)
Example 5-6. A Chemistry 230 student finds that he has sodium carbonate in his unknown sample to the extent of 35.3±0.4% What do you think about the relative precision of this result based on the precision of the equipment we use?
(To be solved in class, again with attention paid to the maximum precision we might expect
to
attain
in this class)
Significant figures and round off
The use of significant figures is ubiquitous in the language of science by virtue of its
convenience.
Its use will be encouraged if for no other reason than that such use provides an easily conveyed
message, a verbal and written shorthand actually, the alternative for which is a mite more
cumbersome. Yet the use of significant figures holds one glaring fault which we must state up
front.
Consider the two absorbances 0.109 and 0.901 taken from a visible absorption
spectrophotometer.
They both convey three significant figures because the rule says that the last digit shall be the one
for
which there is some uncertainty in the reading, usually the interpolated digit. Yet, at the most
optimum, both would have an uncertainty of ±0.001 so that the relative uncertainty of the
first would
be almost nine times larger than that of the second:
![]()
and
![]()
That having been said, let's take a look at some examples of typical reported values and our
responsibility as scientists in offering reported values.
If you as a scientist report that a soluble sulfate unknown contains 21% sulfate, that report
conveys
to the recipient the understanding that the determination is in error by at least 1%, that is
21±1%.
It might be off by 2% or 3%, but the last digit in the reported value is an indication of where the
uncertainty lies. The fact that we DON'T KNOW what the
uncertainty actually is, unless it is
explicitly stated, represents a second defect of the use of significant figures. On the other hand, a
student in Quantitative Analysis ought not to report 21.0% or 21.000% if the value was known
only
to ±1%. This would convey some serious confusion to the recipient of the report, not to
mention a
perceptual error on the part of the student. If the student knows the percent sulfate to a
hundredth
of a percent, that is, if the calculations with uncertainty taken into account yielded the value of
21.37±0.04% sulfate, the student certainly ought not to report 21% because the value is
known much
more precisely than 21% and the report ought to reflect that.
That's fine for the investigator making the report. How about the recipient? As stated above,
the
recipient is to assume that any value presented will be offered according to the same rules, that it
will
be reported to the first uncertain digit.
With that as a jumping off point, the fundamental rule of significant figures is to report any
value to
the first digit for which there is some uncertainty and that uncertainty must be
reported. If it is not,
then one is left rather helplessly to assume some unknown uncertainty in the last digit.
The numbers 0.237, 4.38, 8.70 and 1.47 × 1023 all have 3 significant
figures.
The expressions of the number 2.67 × 10-3, 0.267 ×
10-2, 0.0267 × 10-1, or 0.00267 all have 3
significant figures because, without actually saying it, the use of significant figures is a way of
reducing the statement of precision to the level of relative error
but without rigor. That is to say,
if we assume for the sake of argument that the uncertainty in any of these values is ±1 for
the digit
"7" then 2.67±0.01, 0.267±0.001, 0.0267±0.0001 and
0.00267±0.00001 all exhibit the same value
for the ratio of the error to the value:
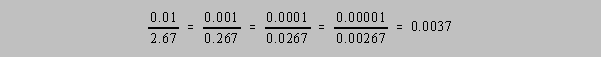
By way of review and emphasis, 3 significant figures means that there is a
minimum uncertainty of
1 in a number that extends from 100 to 999. So the uncertainty could represent anywhere from
0.1%
(1/999 x 100) to 1% (1/100 x 100) of the value. But it gets worse. Saying, "My value is good to
three significant figures" doesn't state the level of uncertainty in
the last figure. In principle it could
be anywhere from 1 to 9. That being the case, three significant figures could show a range of
uncertainty from 0.1% (1/999 x 100) to 9% (9/100 x 100). That is the primary reason always to
state
your values with the added qualifier of the uncertainty itself, as 547±6. That, then, nails
down the
extent to which a reported value can be trusted.
There is one other rule regarding significant figures which must be mentioned here. That
deals with
integers ending in one or more zeros. The rule of thumb is that
these numbers are precise only to
the last non-zero integer. Saying "The distance from the earth to the moon is 239,000 miles can
be
assumed to mean that the reported distance of 239,000 miles may have an uncertainty of 1000 to
9000 miles. If stated as 239,200 miles, one would take that to mean an uncertainty between 100
and
900 miles. If a writer (for example, a newspaper journalist) is forced to use integer notation to
express a large whole number, then the trailing zeros must be there to establish the magnitude of
the
number, not necessarily its significant figures. It is for that reason that large integers ought
always
to be reported in scientific notation where there is little room for doubt: 2.39 x 105
miles leaves no
room for doubt that the uncertainty of this figure starts at the position of the digit "9". The best
way to report a number would be in any case to include the uncertainty, for example, 2.39
±0.02 x 105 miles. The
rule of
thumb means "for most practical purposes." Rules of thumb always have
exceptions. First of all,
there are the definitions of sizes of units. That there are 1000 mL in a liter is a definition. The
relationship is exact. There is no uncertainty. Secondly, there is always the case where some
experimental value in the form of a large integer will come out with trailing zeros -- a vote count,
for example. If the total number of voters turning out in one precinct is determined to be 23000
simply by the luck of the draw, one would not be justified in saying it might have been 24,000 or
then
again perhaps 22,000. If the total was the result of three counts one could assume that it is either
a
valid exact number, or at the very most unreliable to ±1 or ±2.
When you participate in
some of our Web exercises,
make sure that you follow the rule of thumb above
to determine your answers, but store the exceptions
somewhere in the back of your mind.
The Distribution of Experimental Data
The model we use to explain the tendency for values
in a set of data to regress toward the mean is that in
any set of readings there are multiple influences
which may lead to error, some within the instrument
itself, some on the part of the skill of the observer. The observed regression toward the mean, or
the
amassing of results somewhere toward the center of extreme readings is said to be due to the
partial
cancellation of some error effects against others. A simplified model to describe why there is
this
regression effect is that of flipping a coin. The coin flip example is not exactly the same as errors
which can go either way in a scientific reading, but it does lead to a result which is self-consistent
with the model, and the example leads to our understanding of the
origin of the normal or Gaussian
Distribution.
If you flip a coin once, it can be heads or tails. What happens if you flip a coin two times and
you call
this double flip the reading or the
event or the outcome? There are
four possibilities for the
outcome: HH, HT, TH and TT. There is a probability of 25% that both flips will end up as
heads,
25% that the two will be tails, but 50% that one will be a head and one will be a tail. If two
heads
are considered to be one extreme and two tails the other, then an even combination of heads and
tails
falls in the middle. When graphed accordingly, one gets:
x
x x x
_____|______
HH HT TT
This gives you an opening which leads to the study of statistics and the normal distribution,
because
it is the influences, sometimes perceptible but often imperceptible, which lead to variations in
any
reading or taking of a measurement which leads to scatter around some mean -- a mean often
populated more frequently than either extreme because of the greater probability that the
imperceptible influences will counteract each other.
Remember that if you actually flip a coin twice, that double flip is defined as the
event, and if you
carry out that event 4 times, you won't be guaranteed to get all of the combinations above in the
frequencies indicated. Those represent probabilities only. Here is a link to an executable file
which
you ought to run to see this effect.
Go to
http://proton.csudh.edu/lecture_help/startcoinflip.html
This program allows you to simulate the flip of a coin up to 100 times for a given trial and up
to 1000
trials. Give it a try and vary the parameters to your liking. Use your wordprocessor to read
and/or
print the output from the file you define. Notice that although there is a clear regression to a
50/50
mix of heads and tails, there is random variance of the mean, back and forth.
Exercise 5-7. Answer the following questions:
1. Execute the program so that the event (called a "dataset" in the program) is defined as 100 flips of a coin and define the number of events equal to 1000.
2. Draw a histogram containing the data produced by the computer program. The x axis should be the number of heads per event and the y axis should be the number of events.
3. Determine the mean number of heads. (There is a shortcut which you must use to calculate the mean. Otherwise you'll be adding numbers of heads all night.)
4. Determine the standard deviation of the number of heads. (In this calculation there is a shortcut which you must use; it is similar in concept to the shortcut in 3, above.)
5. It is often said in books on applied statistics that the probable difference between x-bar (the mean of a small sample) and mu (the mean of a population) decreases rapidly as the number of measurements in a sample increases and that by the time the total number of observations in the sample reaches 20 to 30, this difference is negligible. There's nothing like an experimental approach to test this claim. First of all, we might ask, just what is meant by negligible? Here are 25 values for the number of heads per event independently generated by the program:
52,53,55,48,55,53,52,54,52,51,46,52,49,51,52,46,52,49,51,50,47,51,46,48,50
Determine the mean number of heads for this smaller sample and the standard deviation.
Would you agree that the difference between the mean for the 1000 generated events and the
smaller sample of 25 events is "negligible?" For the purpose of this exercise, "negligible" is
defined as less than one standard deviation.
This exercise gives you data clearly exhibiting the beginnings of a normal curve which
illustrates the
scatter of an infinite number of readings over a finite range in which there is a significant
frequency
of events; within this range is a smaller segment which includes 68% of all events and is
bounded
by
the location of the inflection points of the population distribution. This defined range is called
the
standard deviation of the population, or (sigma) and its value on either side of the
mean
encompasses 68% of all readings. A distance of two standard deviations or 2 sigma,
encompasses 96% of all readings.
The population mean,mu , and the sample mean, x bar
Here we have three figures. The first, on the left,
shows a plot of the normal distribution function
with a population mean, mu , equal to 50. The figure on the right shows the
same distribution function
except with the abscissa in units of z=(x-mu)/sigma . By normalizing, or dividing by the value of
, each
unit along the abscissa is equivalent to one standard deviation
of the population. The third figure, on the left shows the
results of 10000
events, each event
the flip of a coin 100
times. Note that the
figure on the left
above has been
adjusted so that the
standard deviation is roughly
equivalent to that shown in the
figure below it.
The population standard deviation, sigma and the sample standard
deviation, s.
The population standard deviation which is an accepted measure of the precision of a population of data is given as
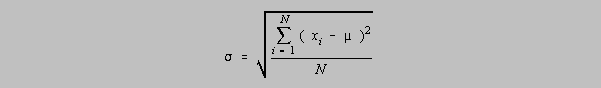
A small sample of data has a measure of precision given by the standard deviation, s, and
uses
a
divisor of N-1 which is called the number of degrees of freedom. It represents the number of
independent data points in the calculation of the standard deviation, s. If mu (the population
mean)
is unknown, then x-bar, or the mean of the sample, must be calculated. It is said that the number
of
degrees of freedom, originally N, is diminished by one by the calculation of x-bar because with
the
knowledge of x-bar there are only N-1 independent data points. Given x-bar, the Nth data point
could be calculated from x-bar and the other N-1 data points.
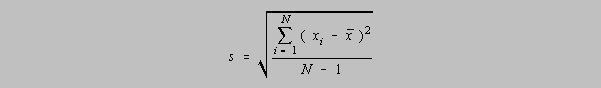
There is an alternative designation for the standard deviation, s, of a small sample, for students
who
do not have calculators with the s function. It allows one to calculate the standard deviation
without
first having to calculate x-bar:
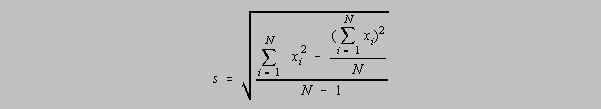
Exercise 5-x1. Prove that the previous two formulas for the standard deviation s are equivalent.
Exercise 5-8. For the whole group. Each student is to flip a coin ten times. Fill in the table.
The
frequency is the number of students who get that result.
| No. Of heads | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Frequency |
Exercise 5-x2. The equation for the Gaussian distribution (the normal bell curve) can take the form
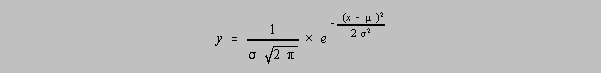
Prove that the inflection point of this function occurs when x=µ±sigma.
Standard error of a mean
The standard error of a mean is given the symbol sigmam in books on statistics and is related to the "scatter" of the means of small samples drawn from a larger collection. For the example below we shall use sm as a substitute for that symbol. The means of small groups taken from a large collection will show a characteristic standard deviation. That standard deviation of the means will diminish as the sample size increases in proportion to the function
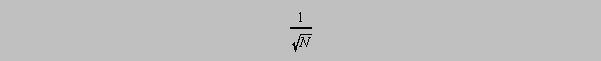
that is, if the
standard deviation sm of the group means is plotted vs 1/(square root N), the values
ought to
decrease linearly and approach zero as 1/(square root N) approaches zero. Let's see if there's any
truth to the claim of linearity.
Exercise 5-9. Here is a table showing what happens if the file coinout.10k with 10000
events,
each event being the flipping of a coin 100 times is read in a manner to calculate means and
standard deviations of small groups of those events. Since the outcome of the events was the
result of randomness and the file itself was not sorted, the groups are chosen in sequence. The
following size of the groups was chosen: 3,4,5,10,50,100,250,500,1000,2500,5000,10000. For
groups of size 3 there are 3333 groups, for groups of size 4 there are 2500, for 5, 2000 and so on.
The mean for all groups of the same size (the mean of the means), and the standard deviation
produced by the individual means within each collection of groups were calculated.
For the class. On the graph paper below, label two convenient scales, putting standard
deviation
along the vertical axis and 1/(square root N) along the horizontal axis. Then plot the standard
deviation of
group means from the mean for all groups against the values of 1/(square root N). How does this
agree with
statistical theory?
| Group size
(N) |
SQRT(N) | 1/SQRT(N) | Mean for all groups | Std. deviation of group means. |
| 1 | 1 | 1 | 50.039 | 4.99 |
| 2 | 1.414 | 0.707 | 50.039 | 3.53 |
| 3 | 1.732 | 0.577 | 50.039 | 2.93 |
| 4 | 2 | 0.500 | 50.039 | 2.49 |
| 5 | 2.236 | 0.447 | 50.039 | 2.25 |
| 10 | 3.162 | 0.316 | 50.039 | 1.58 |
| 50 | 7.071 | 0.141 | 50.039 | 0.68 |
| 100 | 10 | 0.10 | 50.039 | 0.48 |
| 250 | 15.81 | 0.063 | 50.039 | 0.31 |
| 500 | 22.36 | 0.045 | 50.039 | 0.22 |
| 1000 | 31.62 | 0.032 | 50.039 | 0.17 |
| 2500 | 50 | 0.020 | 50.039 | 0.13 |
| 5000 | 70.71 | 0.014 | 50.039 | 0.11 |
| 10000 | 100 | 0.010 | 50.039 | ---- |
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
The results of several experimental determinations and the subsequent calculation of the
standard
deviation says nothing about the true
value. It is a measure solely of the reliability of the method
being used. There is nevertheless what appears to be an irresistible tendency following some
determination in analytical chemistry to link the standard deviation between individual
determinations
with their "trueness," but that tendency must be resisted. The standard deviation between
individual
determinations says nothing about the possibility of systematic error in the determination. It is
the
reliability of the method which is reflected by s.
Standard deviation from pooled data
Rather than simply relying on some average standard deviation for several small samples of
data,
statistical theory tells us that we can go one even better. We can determine a
standard deviation
from pooled data even though those data may represent determinations on
different unknowns. Consider the samples of carbonate analyzed by CHE230 students during the
fall semester, 1999. Four unknowns were used, so there were four different % sodium carbonate
values to be determined. But the same method was used for each. The level of precision would
be expected to be the same for each unknown, even though their percent sodium carbonate values
were widely separated. So the mean percent sodium carbonate is of no great concern, but the
precision, in principle, ought to remain the same. The formula which allows us to determine a
more characteristic standard deviation of the method, from pooled data, is
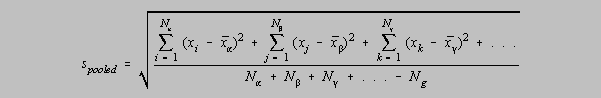
Nalpha is the number of elements in group alpha, Nbeta is the number
of elements in group beta, etc. and Ng is the
number of groups that are pooled.
Exercise 5-10. During the fall of 1999, the following results were obtained from students
carrying
out the determination of sodium carbonate in samples of soda ash:
| Student | Sample 1 | Sample 2 | Sample 3 | x-bar | s | SUM(xi - xbar )2 |
| 1(alpha) | 39.46 | 39.50 | 39.32 | 39.43 | 0.09 | 0.0179 |
| 2(beta) | 29.60 | 29.60 | 29.49 | 29.56 | 0.06 | 0.0081 |
| 3(gamma) | 22.09 | 21.74 | 21.98 | 21.94 | 0.18 | 0.0641 |
| 4(delta) | 40.15 | 40.27 | 40.22 | 40.21 | 0.06 | 0.0073 |
| 5(epsilon) | 20.88 | 20.98 | 20.81 | 20.89 | 0.09 | 0.0146 |
| 6(zeta) | 38.91 | 38.94 | 38.90 | 38.92 | 0.02 | 0.0009 |
| 7(eta) | 32.38 | 31.84 | 32.88 | 32.37 | 0.52 | 0.5411 |
| 8(theta) | 38.19 | 38.18 | 38.18 | 38.18 | 0.01 | 0.0001 |
| 9(iota) | 48.88 | 48.83 | 48.27 | 48.66 | 0.34 | 0.2294 |
| 10(kappa) | 28.74 | 28.77 | 28.76 | 28.76 | 0.02 | 0.0005 |
| 11(lambda) | 49.90 | 49.81 | 49.79 | 49.83 | 0.06 | 0.0069 |
| 12(µ) | 50.42 | 50.38 | 50.45 | 50.42 | 0.04 | 0.0025 |
Using the equation above, determine the pooled standard deviation. Note that the mean for
each set
is used only to determine the square of the sum of the deviations of each result and that
the overall
mean is of no importance where a pooled standard deviation is to be calculated.
Exercise 5-10x. Write a computer program to determine the pooled standard deviation of the
data in the file coinout.10k. With group sizes set at 2, 3, 4, 5, 10, 50, 100, 250, 500, 1000, 2500
and 5000. Comment on the values you receive and comment on differences you observe with the
standard deviation of the means offered in the table earlier in this chapter.
There are some alternative terms used for expressing the precision of sets or groups of data
elements.
They are important to know.
The Variance, s2
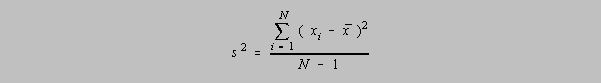
The Relative Standard Deviation
The RSD is
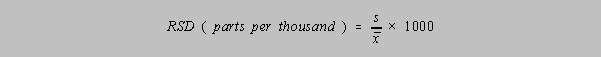
The Coefficient of Variation, CV is simply the RSD in percent:
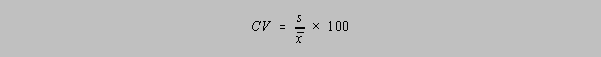
The spread or range, w, is simply the difference between the
lowest and highest values in a data
set. There is a convenient table to estimate the standard deviation using the value of
w. It is
suprisingly in agreement with the calculated value for many applications:
![]()
| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| k | 0.89 | 0.59 | 0.49 | 0.43 | 0.39 | 0.37 | 0.35 | 0.34 | 0.32 | 0.32 | 0.31 |
Exercise 5-11. A water well known to contain particularly high levels of iron has five samples drawn for spectrophotometric analysis. The results show the following levels of iron in parts per million:
134, 147, 125, 131, 152
Determine the mean, the standard deviation, the variance, the RSD, the CV the spread and
the
estimated standard deviation from the table above.
Exercise 5-12. A Quantitative Analysis student determines Cu in brass and obtains the
following
percent copper: 87.85, 87.70, 87.95, 87.78 and 87.65. Calculate the same quantities requested in
Exercise 5-11 above.
Determining the calculated uncertainty from individual
values
The model used for the determination of the calculated uncertainty from individual values
comes
to us from vector algebra and is based on the assumption that if two values are to be added
together, the factors resulting in small uncertainties are not linked. That is to say, a positive error
in some mass reading would not somehow lead to a positive error in a later volume reading.
Moreover, this model applies an estimate that there is a "most probable" error in which there
might be some cancellation of effects which bring about the uncertainties. For example, in
determining the anticipated error in four truckloads of oranges, each with an uncertainty of
±10
oranges, one would not assume the most probable error for the total load to be ±40 oranges
because of the effects of probable cancellation of the total uncertainty between truckloads. In the
final analysis, the two formulas used, one for addition and subtraction and the other for
multiplication and division ought to be considered to be "best estimates" of anticipated calculated
errors:
For addition and subtraction: Consider the operation y=a+b-c+d. Since uncertainties are
considered to work in either direction symmetrically, the sign of the operation is unimportant and
the function giving the uncertainty in the operation, vy is (we shall use v here
instead
of s because
the uncertainty expressed in each parameter may or may not be a standard deviation).
![]()
Note that this formula is the diagonal of a 4-dimensional rectangular solid. It is felt that such a
function gives a more probable estimate of the uncertainty owing to some cancellation of error
effects rather than that which would be achieved simply by adding all of the uncertainties
together.
In other words, it would be overkill on error estimation to state that vy =
va + vb + vc + vd , because
of the presumption of partial cancellation.
For multiplication and division, the formula comes to us from both a vector algebra approach
as
above and a differential calculus model (be forewarned that the calculus model is something of a
finesse to get to the rationalization used above for addition and subtraction calculations):
Consider the operation
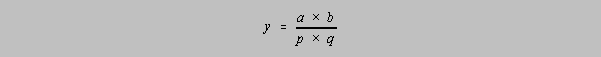
Taking the natural logarithm of both sides, one gets
![]()
The derivative of ln y yields
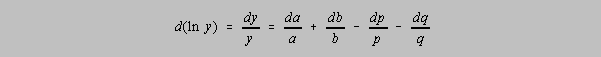
This form is then estimated to be the relative uncertainties in each
case:
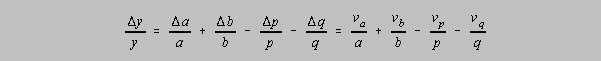
But since the relative uncertainties are assumed to be symmetric around the determined values
and
can work in either direction, these relative uncertainties are added together regardless of the sign
in the derivative. Moreover, since the most probable error would
result in some cancellation
between the errors, following the model used in addition and subtraction operations above, the
form for estimating the error in a process of multiplication and division is (substituting v for in
each case)
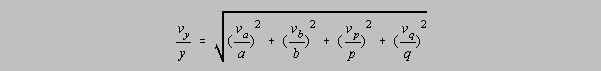
When a problem involving all four operations is to be solved, the uncertainty in the final result
ought to be calculated in the same order as the calculation of the result.
Some exercises in significant figures
For the exercises below, consider each number presented to be precise to ±1 in the last
digit.
Exercise 5-13. The sum of 3.4 + 0.020 + 7.31. To how many significant figures ought the
result be reported and what is the calculated uncertainty?
Exercise 5-14a. Consider the operation (consider all factors to be experimentally determined)
(38.5 x 27)/252.3. To how many significant figures ought the result be reported and what is
the calculated uncertainty?
Exercise 5-14b. Consider the operation (again, all factors have been determined
experimentally) (24 x 4.52)/100.0. To how many significant figures ought the result be reported?
The rule of thumb for multiplication and division is to report
the result to the same number of
significant figures as the smallest
number of significant figures in any of the original factors, but problems arise if the result just
moves beyond 1xxx.xxx or drops just below 9xx.xxx. (To be explained in class)
Rounding rules
If the digit following the digit to be rounded is 6,7,8 or 9, round to the next highest digit. If
the
digit following the digit to be rounded is 0,1,2,3 or 4, do not change the rounding digit. If the
digit following the digit to be rounded is 5, round to the even integer.
Exercise 5-15. Consider the following experimental values. An experimental value might be
a direct observation or it might be a calculated value based on experimental observations. Next
consider the estimated uncertainties. Report each experimental value as one ought to report it
based on the uncertainties. State the number of significant figures indicated by the reported
value.
Calculate the relative uncertainty in percent in each case.
| Experimental value | Uncertainty | Reported value | Sig. Figures | Relative uncertainty |
| 3.827 | ±0.04 | |||
| 0.08831 | ±0.02 | |||
| 0.0243 | ±0.003 | |||
| 2000 | ±10 | |||
| 3.85 | ±0.02 | |||
| 8.735 | ±0.01 |
Significant Figure Rules with Logarithms
Two rules to remember here. (1) The logarithm ought to be reported to the same number of
digits after the decimal point as there are digits in the original
number, and (2) when taking an
antilogarithm, the antilogarithm ought to be reported to a number of digits equal to the number of
digits after the decimal point in the logarithm.
These rules work in most cases. When in doubt consider the relationship y=ln x. The question is what uncertainty in y ought to be reported, knowing the uncertainty in x? Consider the calculus notation:
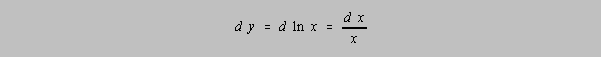
How does that work in real life?
Consider ln 2475 = 3.3935752 with x = 2475 ±1.
dx/x is approximately equal to (delta x)/x=1/2475 = .0004040,
which is approximately equal to y, so ln 2475 = 3.3935752±0.0004040 or
ln 2475 = 3.3936±0.0004. The rule above is followed.
APPENDIX A. The contents of Coinout.10k. If you don't like the idea of running an
unfamiliar
program to select a certain number of data points then tack this sheet up on your wall and throw
darts at it the number of times equal to the number of data points you need. Pick the number
closest to each point where the dart hits. Be careful not to hit your roommate.
49 59 47 49 45 48 51 51 59 58 49 45 58 57 50 56 43 40 52 47 49 53 57 51 52 42 48 41 50 41 50 54 48 59 51 51 50 47 49 47 44 46 48 49 46 50 56 49 53 57 52 46 46 54 49 50 54 47 64 50 51 54 57 55 41 49 44 47 53 42 49 58 54 51 41 45 52 54 49 50 46 49 52 47 47 60 45 56 50 46 50 46 51 48 54 54 53 54 44 49 52 41 57 50 55 56 51 46 51 56 53 53 50 50 52 54 52 61 45 40 54 53 53 53 60 59 54 49 49 51 56 46 53 60 52 47 52 48 50 53 47 60 48 53 44 44 55 43 53 48 48 45 56 43 55 48 45 47 49 48 42 54 49 47 44 42 52 38 56 43 50 43 51 57 44 48 57 55 51 48 52 49 48 40 45 53 50 45 51 52 52 44 52 48 52 52 47 46 42 54 49 51 50 56 50 47 51 53 55 51 43 47 52 39 52 53 60 45 47 48 46 52 40 56 50 51 50 62 59 41 48 55 53 52 51 45 47 51 42 44 50 52 48 63 52 50 48 52 51 42 57 40 59 47 43 48 56 53 51 41 41 48 54 51 51 52 49 50 49 49 47 48 45 44 52 45 49 49 38 56 42 43 43 38 52 51 60 52 58 56 54 52 54 42 54 48 54 48 52 36 54 50 59 52 48 46 57 42 44 57 50 56 47 55 55 51 53 47 55 48 52 50 54 59 50 46 54 43 49 55 55 52 51 52 53 58 54 52 45 51 48 53 56 49 55 51 55 53 46 51 52 49 52 40 46 53 49 66 56 42 50 61 57 49 45 46 50 49 53 50 51 48 57 51 61 44 55 44 62 51 51 49 59 46 49 50 47 51 50 54 50 49 53 47 53 49 58 43 45 45 50 39 46 62 50 51 49 57 49 57 52 52 53 49 53 45 57 60 47 54 49 44 52 50 49 48 54 58 47 54 53 44 54 57 49 56 51 52 49 49 46 50 53 53 43 58 57 54 58 54 41 45 43 47 57 46 47 54 50 54 52 49 45 54 45 49 54 40 55 54 53 47 48 39 48 44 58 42 49 53 50 54 55 54 44 51 50 55 53 53 58 50 55 46 62 48 51 44 46 57 47 45 46 51 46 53 68 35 52 47 56 51 53 57 49 61 58 52 53 43 55 58 46 47 48 54 51 40 52 52 53 47 49 51 53 42 51 48 54 55 43 44 40 58 50 47 48 56 55 46 50 51 50 42 50 52 57 55 49 45 48 55 54 52 35 41 58 49 42 53 48 62 51 43 54 50 50 45 40 53 49 46 51 48 47 47 50 49 53 49 47 53 50 52 51 55 47 52 53 46 50 56 57 49 52 56 41 45 49 44 52 46 57 55 44 41 54 49 51 55 58 49 49 52 52 43 54 45 48 52 45 46 60 42 42 53 52 54 61 48 38 59 45 56 51 50 49 59 43 48 59 53 59 61 52 51 46 49 58 58 55 44 45 47 55 53 49 46 51 49 47 50 37 58 50 45 57 53 49 60 53 45 49 49 51 48 44 51 62 56 51 52 48 47 48 53 51 44 50 54 48 57 46 41 42 41 46 57 49 49 58 53 50 43 46 50 52 52 52 54 54 53 46 43 46 43 49 54 50 55 53 60 56 47 48 59 56 46 49 39 53 51 50 54 56 51 57 44 45 50 46 51 50 48 44 47 44 43 58 53 49 53 60 48 51 51 53 45 58 50 55 48 51 37 44 48 54 45 47 51 53 52 47 47 48 55 47 57 45 48 43 52 57 42 47 48 41 45 50 50 58 53 45 44 54 60 49 50 56 48 43 54 54 49 51 51 51 48 39 53 48 50 50 58 47 46 54 50 40 56 51 49 55 53 53 51 52 43 53 59 52 50 52 51 40 51 44 53 48 48 53 57 40 48 51 49 55 54 49 54 46 62 55 48 51 58 46 49 55 47 57 59 48 48 47 45 47 47 56 56 57 47 43 49 44 54 45 51 56 56 46 51 47 58 58 57 53 44 50 44 51 45 56 52 52 50 47 58 54 52 42 52 47 51 53 46 49 53 56 48 53 47 52 55 45 51 57 49 52 57 50 49 49 49 42 51 56 47 45 50 46 59 50 49 42 57 48 54 57 50 55 52 58 48 52 48 55 47 53 55 53 41 57 53 50 47 59 45 48 43 56 53 47 41 43 46 46 49 56 53 56 51 42 50 47 46 50 50 48 42 47 56 56 50 44 53 51 47 57 54 54 45 51 51 51 51 47 48 53 46 44 46 50 48 55 48 44 46 54 57 66 50 50 47 47 45 48 45 43 53 53 57 48 44 46 45 55 57 47 50 50 41 52 51 47 54 53 53 52 45 53 57 49 46 48 44 57 52 58 53 58 60 53 50 51 64 51 49 52 47 55 45 48 47 57 45 51 37 45 38 53 49 48 56 42 46 48 52 44 47 47 49 57 48 57 46 55 52 55 46 62 41 51 49 41 54 53 46 55 36 50 50 46 52 50 55 51 53 50 51 54 52 52 42 37 48 59 53 50 50 50 46 48 53 47 40 56 54 53 48 52 52 57 53 54 44 46 54 48 45 52 48 46 48 47 51 56 54 51 43 51 46 56 52 45 47 50 44 45 53 57 53 52 51 49 49 44 50 48 56 48 52 43 43 56 46 56 53 46 47 55 53 49 48 54 52 48 53 48 56 62 51 45 44 51 48 50 51 46 45 46 44 57 46 50 53 47 43 54 59 40 56 55 52 54 44 46 50 48 53 53 56 45 47 48 54 45 58 48 52 50 51 48 51 56 44 56 44 55 53 47 48 43 43 46 49 53 52 50 53 52 48 50 51 53 50 63 42 53 46 45 46 54 50 43 51 59 44 55 57 53 49 44 46 57 49 52 53 48 54 53 43 47 52 51 45 48 47 52 50 48 56 46 46 50 52 58 53 49 41 48 48 38 48 53 43 51 46 46 54 50 39 64 53 51 43 52 51 47 57 52 50 49 48 46 55 45 49 41 54 52 54 47 49 58 51 54 48 56 50 52 49 44 53 55 51 43 46 58 54 50 55 60 51 46 51 50 43 56 52 49 37 51 47 59 61 51 52 52 48 43 46 50 45 51 47 56 58 48 49 45 49 40 49 46 50 51 63 44 50 55 53 36 42 58 57 56 51 53 52 40 50 46 52 53 46 59 41 47 52 53 43 48 44 48 48 58 48 46 42 47 64 45 48 52 43 51 56 48 51 52 61 47 53 47 53 54 47 52 50 46 50 45 55 44 50 57 49 49 46 47 55 40 49 50 53 53 50 51 50 57 43 55 40 43 50 52 50 53 50 45 50 58 55 53 49 43 53 45 50 49 46 55 46 52 47 45 55 49 50 49 51 56 44 48 56 50 53 45 46 44 57 50 47 53 48 41 49 44 59 49 53 53 59 45 42 39 58 58 57 43 45 52 43 57 47 58 50 60 47 50 50 53 49 50 53 53 47 45 48 61 48 44 49 51 48 58 42 47 57 49 49 47 45 41 56 51 46 50 52 55 49 57 44 49 43 56 45 54 49 49 48 50 51 54 60 61 45 55 61 41 55 52 45 53 47 46 46 59 49 58 51 51 53 43 42 49 55 50 63 54 46 46 46 48 49 52 56 46 50 40 53 57 45 48 51 53 50 56 52 47 44 55 47 63 50 53 43 45 40 71 44 51 49 60 47 44 50 52 45 46 42 57 50 47 44 56 50 50 54 46 59 59 59 50 59 47 55 48 47 51 50 49 49 48 53 50 57 49 49 49 56 49 45 45 53 45 52 54 44 51 46 45 49 55 44 51 53 48 44 54 46 46 53 47 48 56 51 40 49 53 49 40 57 57 37 50 52 36 43 62 54 54 50 51 52 49 43 51 53 53 53 44 52 45 44 48 50 46 46 46 46 50 51 45 54 55 62 45 50 55 58 53 53 53 49 54 51 46 44 55 41 48 52 48 49 56 37 57 55 55 51 54 47 49 48 51 47 52 45 46 54 46 49 55 52 53 35 54 48 51 47 63 50 52 48 56 44 48 54 44 50 54 52 54 48 45 49 53 46 49 52 45 48 52 50 52 43 45 49 43 51 54 40 43 51 51 53 51 53 45 52 57 50 46 48 52 49 53 53 48 46 49 47 55 49 45 53 50 48 51 56 52 41 46 58 58 47 47 58 49 41 52 44 40 41 50 54 54 52 59 60 56 54 54 52 48 42 54 42 62 39 48 50 42 51 52 48 56 55 56 45 52 53 51 50 51 57 54 42 51 49 44 47 54 55 50 44 43 51 49 55 47 54 52 51 48 47 47 51 49 49 43 47 55 49 48 52 52 45 46 52 55 48 56 51 48 56 52 44 52 48 53 55 48 49 52 47 62 54 46 56 57 63 56 53 48 51 55 47 57 52 51 53 52 46 51 51 50 49 51 48 54 49 44 58 45 52 54 46 47 49 50 49 65 57 47 51 51 47 48 53 35 60 57 51 49 51 53 44 45 59 53 53 53 49 56 55 50 46 51 43 46 56 48 48 56 57 57 51 49 47 54 43 49 51 40 59 45 53 54 53 52 55 54 55 55 50 54 43 57 51 51 52 53 48 54 50 50 48 55 47 51 50 46 55 43 49 52 54 49 52 47 48 45 36 55 53 58 53 48 45 46 52 48 46 50 51 46 49 55 50 47 57 60 52 56 54 55 49 46 50 45 50 53 45 58 45 50 48 51 54 50 50 54 44 58 49 48 53 48 49 52 49 53 47 52 52 54 50 48 55 54 56 56 47 57 50 45 60 57 47 60 54 52 45 40 50 49 50 55 50 48 48 52 49 45 47 45 53 53 56 54 53 53 51 40 54 50 47 45 58 52 52 49 48 49 50 42 52 50 54 57 48 52 50 48 56 52 52 56 50 37 48 48 59 49 52 47 52 49 41 50 53 59 49 46 55 51 46 49 48 58 48 48 50 50 43 53 51 56 51 42 50 51 60 47 48 53 57 60 55 50 50 48 50 46 51 47 47 47 57 53 51 48 51 45 48 51 46 39 52 47 48 48 55 50 43 55 46 42 50 47 64 54 53 50 45 51 48 39 52 49 55 41 50 51 51 43 55 47 55 48 56 45 56 57 45 57 44 50 51 61 52 52 40 42 56 54 49 53 50 43 50 54 51 54 48 53 52 52 47 44 51 47 45 51 56 43 54 54 43 50 49 47 45 47 56 54 42 58 38 52 56 55 55 45 54 50 51 56 51 52 50 45 51 52 57 50 55 47 45 52 47 52 51 54 56 58 51 54 52 48 57 49 43 48 50 51 41 47 44 51 45 59 50 54 51 55 53 41 47 46 49 56 52 54 55 48 46 48 52 48 61 52 49 61 49 48 52 41 60 50 50 52 54 52 46 47 42 50 45 47 57 54 63 57 48 56 45 50 58 61 52 57 54 47 57 46 58 46 46 52 56 51 48 36 52 50 51 62 50 50 49 52 46 49 51 51 43 44 56 52 53 51 56 60 52 46 45 53 55 54 49 51 44 56 48 54 49 54 49 52 56 48 48 57 41 47 40 48 55 48 43 50 52 47 49 56 49 48 50 49 48 49 47 43 45 59 45 53 38 45 45 56 59 56 61 55 43 54 47 45 55 56 55 56 51 57 53 42 51 59 57 51 48 57 45 49 45 49 52 43 59 59 54 50 41 56 45 50 49 42 62 53 48 53 47 47 42 53 52 49 38 52 45 51 46 47 55 48 51 59 44 54 45 45 45 52 49 53 41 52 48 54 47 51 52 48 52 55 55 51 49 48 50 47 52 48 59 53 50 59 43 50 54 42 49 44 44 46 54 47 54 56 59 43 51 44 48 50 55 42 49 47 47 46 47 45 45 49 41 49 55 43 58 44 46 51 45 53 56 51 50 42 56 49 52 60 49 44 45 47 41 45 47 39 45 50 52 58 48 53 49 60 48 52 58 54 46 53 52 51 51 46 55 50 58 46 49 49 48 45 46 50 49 54 56 43 58 44 60 56 55 54 55 42 45 52 45 47 46 52 49 45 44 52 42 56 49 48 50 44 54 52 44 58 52 54 37 53 61 60 42 43 52 40 49 55 59 50 56 50 43 53 51 58 42 52 45 49 50 47 56 46 47 59 52 49 49 45 49 50 53 49 55 63 51 46 50 45 51 54 57 46 55 54 50 46 47 51 50 51 53 41 47 54 55 53 53 51 48 44 57 54 54 53 43 57 61 45 51 53 59 61 52 56 47 54 46 44 52 48 48 52 48 46 54 52 50 46 45 49 45 48 50 48 54 52 46 53 49 52 47 48 47 47 54 52 53 46 57 44 48 53 46 47 46 51 48 51 53 55 57 56 51 46 44 50 48 47 47 45 53 52 58 52 47 51 59 46 54 61 51 48 44 49 52 60 44 55 47 55 45 60 48 52 51 56 48 49 65 39 46 54 51 47 51 49 56 55 55 45 45 47 48 49 43 46 52 44 44 39 52 52 41 43 43 49 48 47 55 50 43 46 57 56 50 47 55 45 44 61 46 59 48 53 42 53 51 52 56 50 49 46 54 46 53 48 60 59 54 46 48 47 51 53 53 50 45 50 56 46 46 52 51 50 55 47 49 51 44 57 53 58 59 53 49 49 55 53 50 54 52 50 50 56 46 45 52 56 51 50 54 49 56 49 43 52 53 52 57 44 45 53 53 48 54 48 52 58 47 46 50 50 56 52 45 41 46 41 55 54 42 54 52 46 47 50 49 51 52 45 54 56 49 51 35 45 45 51 58 55 54 54 49 49 50 55 49 50 52 53 57 51 52 55 53 51 48 52 45 51 47 49 51 50 57 47 52 47 53 47 48 55 53 48 45 44 53 56 55 57 36 58 47 46 43 41 47 46 50 47 58 53 54 45 53 48 49 45 54 55 41 50 53 48 49 52 54 51 50 55 57 47 47 45 57 52 55 48 46 43 56 43 51 43 56 46 49 43 49 47 57 50 61 41 51 55 52 52 41 52 51 56 47 56 60 38 57 46 54 53 47 49 43 53 50 48 48 58 50 51 40 52 51 39 47 50 54 60 52 52 52 54 48 56 55 51 51 51 48 52 46 45 56 50 52 60 50 54 44 59 47 51 51 47 56 47 44 43 51 58 45 48 51 50 47 49 51 52 45 58 47 53 49 43 52 49 56 58 48 55 48 44 54 53 53 53 51 50 49 43 46 55 50 49 53 45 51 52 50 47 50 47 59 50 52 49 50 61 51 47 42 49 46 42 54 51 58 46 47 46 53 50 53 53 50 44 53 54 53 55 45 49 57 51 53 39 55 51 53 46 49 54 51 51 46 51 44 54 49 43 55 42 51 46 56 52 55 48 40 41 51 56 48 59 53 44 51 46 42 48 55 50 48 54 39 48 50 55 51 53 49 50 48 48 51 48 44 46 53 53 42 48 58 47 51 50 44 49 53 54 47 48 45 60 44 39 59 37 45 48 55 45 49 66 51 48 56 53 55 39 52 54 54 56 45 49 45 47 39 54 52 57 48 54 58 52 42 49 50 47 56 52 49 49 47 55 43 58 53 41 55 42 46 60 59 51 46 51 53 44 39 51 44 48 50 52 47 53 50 63 49 55 57 48 48 52 47 40 60 48 57 44 51 47 51 49 56 42 58 49 51 52 52 44 56 53 54 47 46 46 56 52 60 56 48 53 53 52 49 50 54 48 50 52 47 53 44 49 46 48 45 43 51 47 60 45 49 46 42 53 52 56 41 42 45 50 52 45 44 48 51 55 58 53 58 50 56 55 50 51 49 45 48 47 52 48 47 59 45 49 56 61 46 40 43 47 50 50 54 54 46 45 51 47 45 58 40 47 48 49 37 49 47 43 49 49 53 47 46 49 41 46 47 48 51 55 44 44 57 43 52 48 57 53 48 45 53 47 45 48 49 55 44 53 55 61 41 59 56 52 53 49 53 55 49 38 52 55 53 41 51 42 54 51 44 47 53 61 44 50 50 43 52 45 47 64 54 48 46 48 39 47 54 45 50 53 56 45 50 54 53 50 61 53 45 47 55 56 64 47 48 44 52 50 50 49 44 50 59 58 42 49 50 44 46 45 42 53 52 48 49 50 52 61 49 50 58 58 56 51 50 49 54 52 58 51 50 36 48 47 50 42 40 49 55 49 52 41 52 60 53 43 55 46 49 47 54 45 46 54 44 49 48 41 55 52 60 53 52 47 46 47 44 46 56 51 55 41 53 47 58 56 49 50 48 53 63 47 45 54 43 51 45 58 52 48 50 59 57 51 61 51 60 48 52 44 46 54 51 51 47 46 53 46 55 48 43 59 50 60 46 51 40 52 38 44 55 52 45 45 51 47 56 42 51 48 47 57 55 47 49 54 48 56 57 52 48 46 55 53 52 50 48 50 58 44 53 49 56 56 43 46 52 52 44 54 49 45 47 52 56 51 49 50 56 47 48 53 42 45 52 49 48 58 54 46 57 42 57 47 52 56 39 42 49 51 46 53 51 50 56 49 56 55 39 48 56 45 49 45 42 49 48 42 47 45 46 50 46 48 53 48 49 50 61 46 47 55 47 51 55 47 50 63 54 48 48 46 50 48 47 59 50 43 51 39 47 48 55 55 49 49 51 50 46 45 47 54 48 48 48 52 50 50 52 50 47 55 52 53 42 45 55 43 44 42 38 48 51 44 42 52 46 43 38 51 45 48 46 43 46 45 45 50 52 48 44 42 49 60 50 58 50 45 44 46 46 56 44 54 47 47 56 44 39 48 47 53 49 49 60 49 50 50 49 54 48 59 48 54 48 47 53 47 46 51 51 45 45 52 52 51 53 50 52 50 39 48 43 49 48 59 50 52 50 55 54 43 44 57 54 46 45 40 53 49 51 46 52 46 53 60 47 46 49 50 53 46 49 52 46 47 50 52 51 50 52 50 53 53 44 48 51 44 54 42 55 46 52 49 54 49 53 53 46 45 51 50 51 45 46 44 46 55 47 50 47 56 53 57 47 52 47 43 52 47 45 52 46 53 47 42 40 47 49 45 46 49 44 53 41 47 46 56 58 43 55 55 50 47 48 47 46 45 45 44 53 44 49 56 47 49 50 50 47 45 46 51 54 44 47 56 47 51 57 48 49 39 52 54 50 40 51 52 48 46 48 59 55 39 56 49 59 53 55 46 51 53 56 62 53 45 48 46 60 49 54 45 51 49 53 60 57 54 53 39 43 46 49 42 61 51 50 46 39 43 50 44 51 49 52 54 64 47 51 56 43 49 52 42 49 46 45 48 44 46 47 52 49 54 52 49 58 49 53 50 53 54 55 54 58 51 55 59 43 48 49 57 49 41 52 50 50 60 43 47 52 50 54 48 46 53 50 54 51 51 43 50 62 55 56 42 55 51 52 55 52 43 53 55 56 53 52 44 46 50 56 55 50 48 47 38 43 51 50 55 47 48 43 46 59 52 51 51 58 54 56 54 46 49 54 51 55 48 60 43 63 49 53 42 42 54 45 57 51 56 52 51 52 47 55 50 39 52 47 54 59 49 55 46 56 45 52 52 56 56 52 56 53 54 52 54 60 52 60 66 60 53 42 52 40 46 42 43 50 46 53 47 49 58 43 49 56 52 60 45 63 41 43 61 57 51 51 55 50 57 51 51 49 44 44 48 43 53 54 55 54 54 52 44 62 52 62 48 51 45 45 41 44 45 55 49 51 49 54 60 54 65 48 56 46 45 51 53 46 46 46 48 53 51 59 53 51 49 50 52 53 46 52 45 53 52 51 53 49 44 46 50 48 50 50 49 56 53 48 45 55 51 45 56 42 47 63 41 59 48 52 53 45 45 48 59 52 50 51 53 53 54 53 52 48 49 50 38 44 47 37 49 47 45 52 50 54 50 46 50 49 49 50 53 53 52 41 43 48 59 60 48 48 56 48 44 58 45 57 50 45 51 51 49 52 51 51 40 49 51 49 48 50 49 58 59 46 53 50 60 53 46 45 48 51 58 58 42 51 53 49 55 50 48 53 52 46 52 61 47 46 46 50 53 58 48 55 49 54 59 48 48 57 47 52 51 48 52 45 51 53 45 51 58 55 57 56 51 50 40 52 53 44 47 47 51 49 58 50 47 60 50 54 40 40 52 48 57 45 49 46 45 56 56 43 44 57 48 49 50 49 51 45 54 43 49 43 44 60 50 45 46 41 53 43 44 51 45 51 53 40 52 48 49 53 42 48 57 51 55 55 49 52 54 58 49 58 48 53 56 44 55 46 47 55 51 51 64 46 39 50 56 35 43 42 51 50 52 52 51 50 51 47 53 53 54 45 51 51 58 49 43 55 47 47 42 50 57 47 54 55 60 49 59 53 53 47 46 51 50 56 53 53 44 47 51 59 63 44 45 56 58 52 46 52 54 53 49 56 53 49 41 46 44 47 44 49 54 64 50 41 46 45 46 47 48 50 39 48 46 55 48 49 48 49 49 48 52 48 44 40 45 43 45 46 56 52 44 43 52 53 50 54 47 40 48 44 63 51 43 48 52 51 55 49 41 37 53 46 50 48 47 57 49 47 41 44 49 58 53 56 53 51 51 53 46 52 45 53 49 54 55 44 60 54 49 57 45 46 50 46 50 58 51 54 52 56 43 50 48 51 52 47 46 49 61 48 47 51 50 50 43 54 38 46 48 53 53 50 61 50 45 49 44 44 43 57 50 44 50 53 57 55 59 56 48 49 48 47 58 55 50 51 54 55 44 54 45 52 53 60 47 49 45 52 51 56 47 56 48 56 52 49 59 55 48 49 51 47 51 36 51 48 56 55 47 52 51 54 46 43 50 54 44 58 52 47 48 63 47 42 56 46 42 51 53 54 40 52 48 46 50 46 47 59 50 51 53 47 54 52 46 51 52 49 49 53 39 43 57 53 43 52 50 52 50 41 45 47 49 52 55 46 57 52 47 64 44 53 52 48 55 55 50 55 41 47 49 51 51 49 51 55 48 53 45 54 49 54 50 49 48 43 51 53 37 57 50 50 59 48 46 54 57 58 53 52 44 50 52 52 52 48 55 52 53 52 50 58 45 48 62 53 46 50 51 38 56 51 52 50 51 51 48 43 44 47 52 49 55 57 50 44 51 43 45 44 55 50 42 51 37 54 49 43 45 52 48 53 52 51 51 53 50 47 51 55 48 51 54 56 56 46 45 48 52 51 49 57 52 46 60 59 46 44 45 52 45 50 41 39 45 54 45 50 50 48 48 47 55 56 51 48 52 40 53 49 46 60 50 53 55 46 51 55 39 54 46 46 51 54 47 48 55 53 55 41 46 45 51 46 52 46 49 58 46 52 49 57 43 54 50 51 52 41 52 37 59 48 53 38 51 49 49 53 56 46 40 43 51 56 55 53 45 45 55 42 36 54 52 54 54 49 54 41 47 59 51 54 51 51 54 56 49 45 45 50 51 55 57 55 41 47 50 47 59 57 49 59 45 48 49 47 50 44 43 43 45 44 43 50 47 53 47 54 56 51 51 50 50 47 51 52 49 42 51 53 55 50 42 44 50 54 53 43 52 50 43 53 59 53 50 58 55 54 43 43 41 39 48 48 53 49 56 50 53 55 43 48 45 55 59 48 50 55 48 48 40 44 53 50 52 47 52 45 47 51 50 54 52 64 56 55 53 43 48 45 52 49 52 53 36 51 48 49 50 55 60 56 48 54 49 56 50 56 48 40 55 45 47 50 51 51 47 49 51 43 48 51 56 43 52 58 59 60 60 61 45 44 41 62 57 53 46 51 51 54 49 50 51 54 47 48 46 46 44 48 47 61 52 47 48 51 46 47 38 44 56 54 41 54 47 55 38 50 50 49 50 47 48 47 45 49 52 57 49 47 50 55 56 39 56 49 44 47 52 53 48 50 44 52 36 47 58 45 58 53 56 49 53 55 51 46 58 53 42 57 60 46 42 49 50 44 50 48 43 48 55 50 56 54 50 54 53 39 49 43 52 52 61 48 44 50 46 40 50 48 50 48 45 46 55 47 49 47 51 50 50 45 59 42 51 46 53 46 46 44 50 42 46 51 56 49 47 43 47 54 57 59 44 55 43 53 47 49 54 46 51 59 44 35 43 51 46 46 47 57 60 49 53 51 50 51 39 50 52 54 47 46 43 57 57 51 49 57 44 47 53 50 53 54 47 43 44 49 51 45 50 51 50 51 50 57 49 49 47 54 42 52 60 56 52 49 57 48 51 54 54 46 49 47 47 55 52 46 50 51 47 60 52 53 60 47 42 53 47 44 52 58 50 51 58 38 40 48 50 51 52 51 51 43 47 55 49 57 51 52 54 47 48 53 45 51 49 47 61 63 52 45 44 54 46 53 47 51 43 54 47 45 53 52 51 39 52 57 51 52 60 41 51 48 50 54 44 47 59 65 45 54 57 52 45 48 46 50 42 49 51 43 48 51 51 58 51 53 46 55 48 42 57 46 53 48 56 49 52 53 49 51 39 57 48 50 48 48 55 52 53 54 53 44 56 49 44 47 47 49 43 57 53 38 50 44 57 47 55 45 52 55 49 55 48 51 52 51 58 45 47 50 48 48 40 53 48 48 48 48 53 43 46 44 46 48 54 56 58 47 50 42 54 58 45 39 53 57 47 50 54 54 66 47 49 47 49 53 46 48 50 49 38 50 50 56 60 56 49 46 49 51 52 49 48 50 44 49 56 43 41 55 47 54 50 53 49 50 47 51 44 51 52 56 60 46 54 59 59 60 50 59 48 49 50 38 55 57 46 54 46 50 45 56 56 47 45 49 58 50 49 45 46 47 47 45 50 54 46 49 49 44 40 52 57 51 56 45 48 52 58 51 55 55 46 46 55 45 51 51 61 50 50 51 56 38 43 48 43 51 58 47 53 49 54 48 39 40 49 55 45 49 47 49 61 44 49 45 45 64 57 55 42 53 49 52 45 50 51 44 58 54 42 45 48 57 43 61 55 41 48 52 48 54 36 47 42 53 56 44 42 40 51 50 57 58 50 55 51 43 54 48 51 53 50 40 49 41 49 46 53 55 56 37 48 51 57 41 49 54 56 38 56 50 52 55 50 40 44 49 54 44 49 46 46 46 39 44 46 57 44 54 58 38 46 48 48 48 39 51 48 59 53 46 50 45 44 49 44 54 57 54 48 53 40 53 55 50 52 54 53 50 47 46 38 55 59 50 44 44 53 49 42 52 40 53 52 58 55 52 45 50 60 47 51 55 52 52 50 53 49 45 49 57 51 56 52 54 47 51 52 53 49 53 48 49 53 56 41 50 50 54 54 51 46 44 50 47 51 52 58 53 47 46 57 39 44 54 52 50 52 54 55 51 49 49 55 51 50 50 53 54 49 50 49 43 48 53 57 56 52 62 50 58 54 50 46 52 59 43 53 61 55 48 54 44 51 48 55 49 43 59 52 51 57 53 51 48 54 49 48 46 52 46 47 48 53 55 48 56 49 51 56 47 41 45 48 52 58 53 48 51 49 48 48 45 58 40 49 48 52 44 60 54 54 52 43 46 53 44 47 48 51 53 55 52 49 49 50 55 49 43 48 52 55 42 53 46 46 60 56 54 55 59 46 48 57 46 52 46 49 57 54 49 56 43 62 58 52 48 52 52 58 51 48 50 52 55 53 47 47 50 48 53 59 55 56 52 53 43 48 49 62 52 42 52 49 52 49 49 57 52 50 57 51 47 48 46 48 47 54 50 45 55 59 52 53 38 44 50 56 54 52 48 51 42 52 56 53 52 54 43 48 47 54 50 56 51 48 53 54 50 47 49 46 51 51 56 52 44 44 44 56 49 44 51 51 50 51 48 44 52 60 54 57 50 53 55 54 46 51 52 55 44 46 54 42 45 42 55 58 57 55 46 43 49 49 53 48 54 53 51 54 47 53 44 47 57 47 49 50 50 57 58 45 55 50 61 44 49 50 39 43 48 56 46 46 45 49 47 40 46 36 48 55 52 47 51 55 52 43 46 55 59 46 53 53 56 56 56 50 46 48 43 39 44 47 55 50 50 46 54 47 44 44 54 45 42 45 46 50 51 46 49 56 50 52 47 49 44 52 54 56 58 47 58 54 51 48 51 56 47 48 47 59 45 49 56 51 55 50 50 54 49 47 63 57 53 43 52 46 44 51 50 56 51 46 48 53 43 52 53 56 53 42 53 53 52 47 45 53 49 46 52 51 46 52 46 54 49 54 52 44 58 48 45 55 57 39 46 51 44 42 38 49 50 43 60 49 53 51 61 43 51 41 49 45 54 44 48 47 44 48 48 60 48 50 40 55 50 57 42 45 59 52 55 45 46 46 43 50 54 50 40 45 42 52 46 41 50 50 53 49 61 51 40 47 53 48 48 59 40 57 46 54 47 51 55 54 52 49 53 43 55 52 54 50 50 39 51 42 56 50 47 53 51 45 48 48 50 46 51 57 55 53 51 44 48 43 43 55 50 41 58 49 53 45 53 53 46 45 49 57 50 45 43 46 51 54 49 45 45 44 51 54 51 61 52 46 47 46 58 42 43 50 59 59 58 58 60 57 52 46 57 48 41 51 39 54 51 41 54 46 48 47 58 47 50 54 53 52 45 43 55 51 44 46 40 48 51 51 50 49 51 53 45 51 53 47 42 58 52 53 56 41 49 49 49 42 43 43 52 48 42 52 52 47 53 49 49 60 43 50 49 46 53 42 44 42 55 55 47 55 49 49 57 43 51 55 54 51 57 40 43 53 43 47 56 53 56 46 55 49 53 44 45 46 47 58 51 48 44 54 48 48 48 46 51 41 52 50 50 50 54 50 58 53 47 39 47 55 49 46 48 48 45 46 49 52 50 51 57 45 46 46 50 48 50 53 54 54 47 47 55 57 53 46 53 59 54 48 51 43 44 46 48 52 59 55 54 52 44 46 50 57 49 51 48 55 48 51 45 48 53 49 56 58 46 51 54 49 44 45 39 55 60 52 61 57 46 48 49 56 45 53 56 43 60 47 39 50 55 56 56 53 52 52 54 46 54 40 40 38 52 46 53 48 43 59 57 48 52 49 55 51 53 41 52 55 48 46 43 42 41 48 51 53 52 49 51 55 56 47 46 44 57 53 49 49 47 48 50 52 44 46 44 49 46 40 47 45 46 46 48 51 55 52 51 53 51 59 46 46 57 54 57 55 55 55 44 50 55 61 49 47 46 53 43 42 48 50 55 56 53 55 44 49 57 43 47 63 57 58 49 57 56 58 45 49 47 48 40 55 45 54 41 51 46 52 44 41 42 48 45 57 49 46 48 44 51 60 58 51 56 52 51 56 48 54 44 56 48 49 55 48 44 46 60 54 41 44 53 54 43 52 52 57 53 57 52 51 43 50 56 57 50 48 46 46 46 51 43 53 50 49 49 64 52 52 50 45 55 46 46 45 45 50 49 50 65 51 51 50 50 52 49 43 44 43 56 51 52 48 56 48 53 53 57 52 53 50 52 50 60 43 47 44 47 49 57 49 50 45 43 50 46 60 53 49 52 45 45 41 52 48 61 50 53 54 52 52 45 49 42 48 59 51 47 50 56 48 50 62 43 33 58 57 51 54 42 45 41 51 53 43 47 53 57 48 49 43 48 59 45 52 47 59 57 49 52 50 51 45 50 53 51 52 49 46 51 48 47 51 47 44 51 47 54 53 50 57 48 54 54 48 49 39 48 51 48 50 49 44 54 54 61 48 61 53 50 46 49 54 47 45 48 46 44 48 43 57 55 44 50 53 58 51 51 50 49 45 43 55 57 45 54 48 50 52 46 47 49 53 47 53 47 54 42 46 49 46 57 53 51 47 56 51 43 52 48 52 54 41 50 49 61 49 53 43 55 52 49 60 57 62 56 45 46 51 46 43 45 59 49 50 51 48 50 42 48 44 55 48 51 49 50 50 46 45 47 44 54 43 52 45 46 58 59 48 51 52 46 45 53 46 44 45 55 45 52 50 43 59 49 48 53 50 48 50 52 52 44 49 51 40 48 64 50 47 46 53 51 47 51 47 42 51 48 55 52 53 45 41 45 58 44 53 57 45 50 52 53 53 46 49 51 51 55 55 53 49 48 50 52 50 46 40 44 51 47 47 48 51 51 55 47 46 53 55 51 42 41 48 48 58 56 51 43 48 44 55 57 48 50 57 45 57 49 52 54 39 41 50 53 47 48 50 51 48 46 53 60 54 60 48 57 45 57 46 54 48 48 47 52 55 48 50 62 54 52 54 57 53 43 45 52 48 54 53 49 61 47 45 50 59 48 52 51 53 43 54 51 53 53 50 52 53 47 57 48 54 50 48 52 50 52 40 40 50 50 51 49 55 50 45 46 47 48 51 57 51 52 44 52 44 47 53 53 59 51 50 53 44 53 50 48 55 49 55 46 55 45 52 49 48 50 51 44 60 52 50 44 50 56 54 58 44 55 44 51 49 46 46 53 49 54 41 55 45 41 47 52 53 43 57 48 43 47 56 58 44 43 62 38 49 36 59 50 54 45 57 54 48 43 45 43 48 53 52 61 51 49 43 52 56 47 53 54 42 53 45 51 52 47 47 59 53 50 51 50 49 46 39 48 49 51 48 51 51 54 49 52 49 53 52 46 46 46 49 43 50 52 51 53 45 51 56 49 45 53 47 53 51 44 45 52 55 52 45 46 53 54 59 50 49 54 42 40 48 47 53 56 49 46 48 47 44 59 47 59 50 45 47 42 38 47 48 45 49 53 55 51 58 52 49 50 43 55 47 43 44 45 43 49 46 51 43 56 51 53 48 50 49 50 45 45 47 47 56 42 41 61 40 45 46 47 46 55 50 54 48 46 57 55 50 50 52 48 51 49 51 39 44 51 56 52 51 55 54 49 50 50 50 57 51 51 53 45 56 54 41 54 46 52 61 48 54 45 41 44 47 56 50 59 41 49 48 38 47 49 49 54 52 51 53 41 46 44 48 46 48 53 54 55 44 56 51 46 53 52 42 53 48 45 53 54 50 55 48 43 54 42 52 50 50 47 55 52 51 51 59 51 50 52 55 59 49 51 54 50 64 56 47 47 50 53 57 45 54 47 56 45 43 53 46 53 49 48 56 46 52 50 57 45 47 49 44 48 44 47 53 48 55 40 53 51 50 49 50 37 50 50 52 54 41 47 46 48 47 49 57 47 54 48 49 51 43 49 57 57 49 46 51 51 51 43 44 53 50 55 53 56 46 52 43 54 45 42 44 37 46 46 54 48 58 51 54 56 51 52 46 52 53 47 50 54 58 48 47 48 55 38 40 48 52 54 58 49 58 52 39 51 55 62 58 47 60 44 47 50 53 59 54 49 52 40 46 47 42 44 55 50 48 51 49 53 51 64 49 55 52 53 61 56 56 49 48 50 53 56 56 51 53 55 49 38 50 51 54 48 54 46 51 60 57 47 46 49 62 44 58 53 52 47 50 59 45 51 49 53 51 51 46 42 47 49 59 43 58 52 58 49 44 49 44 52 45 52 51 51 48 48 44 55 46 42 46 52 49 57 46 47 61 44 58 51 54 55 43 52 50 49 49 53 60 55 54 49 45 47 46 48 46 54 53 50 49 53 42 49 48 47 44 55 58 59 47 54 45 47 57 51 49 53 43 53 47 51 47 53 49 55 51 54 49 54 52 55 46 49 47 46 57 48 55 45 50 57 48 57 44 50 49 52 53 51 60 57 51 61 50 50 46 49 45 47 53 47 53 44 55 45 55 53 53 52 50 61 45 52 46 46 51 52 54 56 52 52 47 51 43 47 42 46 48 51 52 51 42 59 44 46 49 48 50 49 41 51 48 55 51 48 52 47 42 50 50 55 53 43 51 50 49 44 39 54 48 46 50 50 50 42 53 40 52 56 57 49 57 43 59 57 43 44 49 46 47 49 50 46 48 52 41 53 52 46 61 51 55 40 39 57 59 48 45 55 48 49 48 51 52 44 56 53 44 52 48 52 50 59 49 54 52 53 57 51 39 43 49 47 55 48 51 51 44 52 45 45 56 42 52 48 53 49 51 37 53 47 52 57 46 47 48 48 51 45 48 54 48 46 44 52 46 54 50 44 58 44 48 51 46 44 47 51 63 52 47 56 56 47 45 54 52 56 49 51 52 46 47 49 53 44 53 53 50 50 50 56 60 59 52 50 51 60 49 52 55 49 48 55 50 53 49 54 48 42 50 54 50 49 44 43 47 38 43 51 47 51 46 51 47 61 53 50 47 43 50 49 51 40 50 58 59 50 43 48 55 45 66 50 55 57 55 48 49 46 59 58 47 53 47 54 51 46 46 44 44 46 49 48 59 53 52 55 52 53 47 49 47 54 56 51 58 48 49 47 52 53 52 55 48 50 46 48 56 58 52 48 46 53 56 53 42 54 56 52 43 48 46 48 50 49 54 54 55 57 49 42 53 46 56 45 51 61 49 52 42 48 48 51 51 50 48 43 46 49 51 55 44 52 45 46 44 58 55 50 47 47 43 51 44 50 50 49 59 48 43 46 40 43 52 54 48 46 52 47 54 56 49 56 48 58 55 54 37 38 56 53 47 49 46 53 52 46 43 51 52 54 45 58 44 49 50 47 48 53 50 42 51 45 52 47 47 44 46 52 50 39 50 53 46 52 48 52 64 48 59 48 50 53 36 54 61 48 46 52 54 51 56 54 40 50 47 49 48 48 50 49 51 51 45 59 47 45 47 48 48 57 49 44 50 48 49 49 48 46 45 52 58 44 51 56 43 51 63 49 51 45 61 45 44 50 54 53 43 51 46 54 48 50 50 57 52 52 45 52 43 42 48 54 54 47 54 50 49 50 56 49 54 47 55 60 45 52 49 53 56 58 57 49 55 58 46 49 45 55 44 44 56 46 38 48 48 47 54 48 58 51 45 53 40 52 48 51 54 46 43 47 58 41 58 53 44 49 49 44 48 51 45 47 46 40 50 48 58 47 54 50 57 58 45 49 54 56 50 52 42 53 51 62 47 44 44 51 52 46 57 54 49 48 47 47 47 42 58 53 51 53 54 52 46 46 47 44 50 55 54 51 39 61 50 53 56 41 51 57 54 61 42 50 46 45 51 45 51 58 45 58 50 50 47 57 49 49 56 40 42 52 45 50 44 56 50 46 53 49 46 59 44 45 43 53 40 48 43 56 52 48 47 53 46 49 58 50 51 45 49 50 54 45 37 49 47 45 53 58 50 54 45 54 44 48 51 53 57 48 50 47 54 41 53 50 48 55 52 53 48 56 47 38 53 54 43 56 40 55 51 52 54 50 55 51 51 55 50 45 46 55 51 49 49 38 47 47 50 58 55 52 52 53 41 50 47 48 49 52 49 48 48 53 45 48 44 50 50 52 43 51 54 52 50 40 54 58 58 50 44 50 37 47 49 43 54 43 57 54 48 43 56 52 40 47 55 51 46 55 48 46 54 46 49 46 52 39 55 41 39 46 51 48 45 50 54 55 54 46 55 47 50 52 55 54 47 48 46 56 48 51 45 46 52 57 56 49 49 42 53 48 55 49 53 53 57 50 41 47 56 43 42 56 56 50 48 47 61 56 41 49 58 45 44 44 43 47 39 45 55 53 53 57 50 49 46 58 44 47 43 46 39 47 45 52 56 52 61 48 58 49 53 50 38 51 48 49 53 48 49 60 41 51 47 50 49 52 57 49 49 41 51 50 49 49 47 57 54 52 55 56 51 42 45 59 48 50 48 52 38 51 47 58 57 56 51 52 53 50 44 52 45 52 51 48 43 53 57 48 47 50 50 60 54 53 59 49 51 46 49 49 42 54 56 44 48 52 39 52 52 46 39 53 40 42 42 46 47 56 56 47 48 41 51 46 50 51 57 53 53 49 58 49 49 55 51 50 46 53 46 46 57 47 54 43 52 63 47 51 55 50 50 50 55 42 44 45 52 53 48 52 57 48 52 47 53 53 58 46 51 53 48 52 49 45 41 52 48 49 48 57 49 44 47 55 51 47 47 45 49 44 45 51 51 48 54 45 52 47 59 55 51 54 51 47 40 50 50 41 50 52 54 43 50 49 51 50 51 52 46 54 52 44 46 46 55 51 62 47 50 56 51 46 51 45 52 51 42 49 48 49 44 54 41 47 45 55 61 44 57 55 53 49 53 57 45 56 45 53 45 48 50 56 50 50 56 42 53 52 46 50 46 49 53 52 56 45 54 50 46 49 54 59 43 58 55 55 48 50 50 45 50 54 49 47 57 54 39 51 49 44 53 47 54 57 51 47 57 48 50 50 53 55 58 50 49 54 44 54 60 54 48 64 46 49 48 48 48 44 51 40 45 46 36 45 48 47 51 50 52 48 46 44 52 54 46 53 62 51 55 54 50 40 54 47 52 55 46 57 45 44 45 50 56 47 47 42 53 51 53 48 47 57 49 57 51 44 48 50 58 55 44 48 47 55 53 53 60 50 51 56 44 47 48 49 61 51 51 50 46 48 46 57 53 58 50 53 52 50 48 44 46 41 53 51 51 50 52 51 46 48 49 54 53 48 50 45 53 50 50 49 56 55 48 53 43 51 44 59 48 47 42 50 48 46 52 38 54 54 40 40 50 52 45 57 46 42 53 57 47 51 46 44 48 53 49 44 49 46 54 51 57 47 52 49 42 49 56 48 54 47 58 51 49 58 46 48 55 57 46 49 40 48 43 52 52 54 49 50 55 39 53 53 43 63 47 47 50 50 44 51 51 55 49 42 51 47 54 42 45 46 56 60 47 48 52 63 50 48 52 43 46 51 49 60 44 50 44 50 47 52 49 42 50 52 47 56 55 53 54 45 45 55 48 46 51 63 54 58 49 50 46 51 44 43 51 40 49 51 47 48 56 44 53 50 37 59 43 62 52 55 46 46 48 49 50 38 51 49 51 49 55 54 58 41 48 47 48 38 48 55 52 56 42 48 53 47 47 56 44 58 44 48 51 59 52 47 49 57 53 42 50 47 44 55 47 57 48 55 49 57 57 52 56 47 45 60 56 49 56 48 43 45 44 56 41 41 45 54 47 50 47 51 47 53 53 55 51 46 48 52 47 48 54 47 55 46 45 53 50 41 51 41 50 53 56 52 52 49 58 54 50 53 52 37 54 55 50 43 46 48 54 49 50 54 57 48 49 49 56 43 39 52 47 54 38 56 51 54 44 51 47 43 59 49 52 53 61 48 46 45 59 46 49 55 44 47 64 55 45 58 48 49 49 44 51 50 50 59 47 34 56 51 61 54 50 44 47 45 58 49 49 55 53 51 47 40 38 48 52 52 45 53 50 46 55 51 46 55 48 52 52 52 46 50 49 57 47 55 58 39 49 53 52 55 55 47 54 52 48 58 56 58 48 50 49 53 47 51 48 53 57 50 44 63 44 57 50 53 49 60 61 57 56 52 55 45 46 55 48 46 50 52 45 52 44 53 47 44 50 47 49 55 48 46 49 54 40 48 46 48 49 57 49 55 54 48 49 56 47 60 44 53 56 49 50 52 56 53 52 58 48 45 51 48 58 54 45 57 58 51 42 54 58 55 57 49 42 56 53 49 53 51 49 52 52 56 45 55 47 51 46 48 46 48 50 59 50 52 49 53 47 50 50 46 45 46 47 50 56 57 46 65 49 55 57 42 55 47 52 53 47 49 54 50 47 53 49 49 43 42 44 48 53 51 49 54 47 55 52 57 45 52 44 49 46 57 56 43 55 45 48 57 46 54 45 58 46 51 54 58 55 50 42 62 54 53 52 44 49 49 44 51 59 40 39 55 52 48 40 58 63 60 46 58 46 43 58 55 44 60 56 47 49 46 55 51 52 45 54 43 48 52 53 52 55 62 57 41 53 55 51 48 57 45 43 51 55 55 37 48 58 60 60 46 55 52 44 49 54 52 48 41 61 44 49 59 47 45 46 38 50 58 51 48 49 50 46 52 57 47 51 43 54 52 47 46 54 53 53 58 52 51 55 51 43 55 48 50 49 48 54 49 52 42 45 59 49 52 48 38 49 50 41 49 48 42 47 55 46 49 51 47 49 54 59 52 48 45 49 53 50 49 54 50 51 47 44 49 46 46 55 46 51 44 50 40 54 48 41 48 50 49 48 51 52 57 54 46 47 55 50 51 46 42 49 50 55 52 44 54 50 49 59 61 51 55 47 51 48 57 49 45 54 52 58 51 51 52 49 53 39 43 46 55 53 59 43 48 48 50 42 48 46 49 52 53 51 51 52 46 59 47 43 50 53 50 54 50 58 48 42 50 47 54 43 46 47 55 51 59 43 47 51 52 50 47 47 44 51 48 52 46 48 38 47 49 49 55 52 55 44 46 51 46 58 46 49 52 56 59 47 53 46 54 51 49 50 53 49 43 59 44 47 48 47 47 53 47 42 52 43 48 54 48 43 49 38 51 51 46 47 50 43 56 48 49 49 50 61 46 52 56 52 53 49 56 59 50 47 50 44 51 56 53 58 56 62 53 50 46 49 47 49 53 50 51 50 50 50 49 45 49 52 53 50 52
1. Feynman, Richard P., "Surely You're Joking Mr. Feynman!", Bantam Books, New York, N.Y., 1985, pp 103-104.